2022. 6. 20. 23:39ㆍ강의 내용 정리/자료구조
Binary Search Tree
1. Tree
1) Graph와 Tree
(1) Graph
- 노드간의 연결관계가 표현된 것
- Tree는 여기에 해당된다. 따라서 트리는 그래프의 특성에 더하여 추가적인 특징을 가지고 있다.
(2) Tree
- 한 노드에서 시작해 다른 노드로 도달하는 모든 연결이 유일하게 있어야한다.
(3) Binary tree
- 이는 트리의 특성과 더하여 추가적인 특성이 존재한다.
- 자식이 최대 2개까지 오는 트리
- 리프를 제외한 모든 노드가 풀로 가지고 있는 경우 complete binary tree라고 한다. 이때 2의 높이 승 -1개만큼 노드의 개수를 가진다.
2) Tree의 특징
(1) Level
- Root node는 0 Level
- 아래로 한 단계 내려갈수록 Level이 높아진다.
- 각 노드마다 각 레벨에 대해 말할 수 있다. ex) 크리스는 레벨 2에 해당된다.
(2) Height
- 트리에서 가장 높은 레벨에 있는 노드부터 루트 노드까지의 길이
- 가끔 루트 노드만 있는 경우도 1의 길이를 가진다고 하기도 한다. 그렇게 하면 Binary Complete tree의 노드 개수를 셀 때 유용하다.
- 깊이가 최대가 되는 경우에는 모든 노드가 자식을 하나만 가지고 있는 경우이다. 최소의 깊이를 가지는 경우는 patially complete binary tree로, 리프노드를 제외하곤 자식 노드를 두개씩 가지는 경우이다. 마지막 노드에 대해서는 좌측 하단부터 노드를 배치한다. 실제 데이터는 2의 n승 - 1개에 딱 떨어지는 데이터만 다루지 않기 때문이다.
(3) Subtree
- 트리의 일부분을 사용해 하위 트리를 만든다.
- 부분집합을 구해서 이를 구성할 수 있다.
- 좌측 자식 기준: Left Subtree
- 우측 자식 기준: Right Subtree
(4) Node
Root node
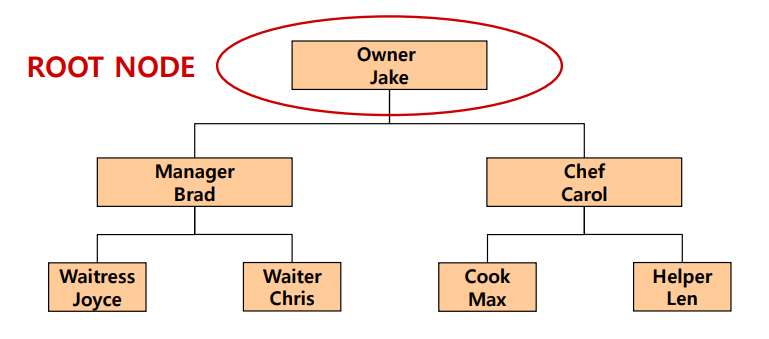
- 가장 상단에 위치한 노드
Leaf node

- 말단에 위치한 노드
- 개념적인 정의 상 자식을 가지지 않는 노드를 의미한다.
- 깊이가 가장 깊은 곳에 있지 않아도 된다.
조상노드
- 루트까지 가는데 거쳐가야하는 노드를 의미한다.
자식노드
- 바로 하단에 위치한 노드
자손노드
- 하단에 위치해 재귀적으로 접근이 가능한 자식노드의 묶음
2. Binary tree
1) Binary tree란?
- 각 노드는 최대 2개의 자식을 가질 수 있다. 자식이 0개도 가능하다. 자식 노드가 0개인 경우에는 leaf node이다.
- 루트에서 다른 노드까지 고유 경로가 존재한다. 이는 tree에 대한 설명이다.
2) Binary tree의 특징
- Height이 최대가 되기 위해선 자식이 1명만 가질 때이다.
- Height이 최소가 되기 위해선 Partially Complete binary tree을 사용하면 된다.
- Partially Complete binary tree: 가장 낮은 단 상위에 있는 노드는 모두 2개의 자식 노드를 가지고, 가장 낮은 단에 있는 노드에는 좌측부터 배치하는 트리
- 데이터를 삽입할 때 루트 노드에서부터 검색하며 더 큰 값은 우측, 작은 값은 좌측으로 이동시키면 Binary Search tree를 만들 수 있다. 하지만 주어진 데이터의 입력이 점점 커지거나 작아질 때는 순차탐색과 다를바가 없을 수 있다.
- 링크드 구조일 때의 탐색 시간과 비교해서 BST는 깊이가 줄어들면 인다이렉션 연산(포인터)의 효율이 증가해 탐색 시간이 더 줄어든다.
- 자식/부모노드는 직계연결이지만 자손/조상노드는 각각 리프노드까지 도달하거나 루트노드까지 도달할 때 거쳐갈 수 있는 모든 노드를 의미한다.
- 깊이가 줄었다고 하더라도 내부 데이터의 규칙성이 없다면 활용할 수 없다. 따라서 깊이가 적고, 규칙성도 있어야지 BST가 의미가 있어진다.
3) Binary tree의 구현
- 포인터를 통해 이를 구현한다. 이때 Doubly linked list와 비슷하다. 각각의 포인터는 좌측과 우측 자식 노드를 가리킨다. 이는 사이클이 존재하면 안된다.
- 링크드 리스트를 통해 구현하지만 이를 사용하지 않는 경우에는 배열을 사용해 구현하기도 한다.
- heap을 구성할 때 랜덤엑세스가 중요하기에 배열형태로 많이 구현하기도 한다.
- operator = 오버로딩은 파라미터에 const&를 붙여야한다. 딥카피를 위해서 이를 사용한다.
- binary search tree는 일반적으로 좌측은 자기 자신보다 작은 것, 우측은 자기 자신보다 큰 것으로 분류하기도 한다. 이러한 특징이 통일되어 트리 전체에서 규칙이 반영되어있어야한다.
3. Binary Search tree
1) Binary Search tree란
- 한 노드에 대해서 더 큰 데이터는 우측에 두고, 작은 데이터는 좌측에 둔다. 모든 노드들에 대해 이 특성을 유지한다.
- 각 노드에는 고유한 데이터 값이 존재해 이를 통해 크기의 대소관계를 비교할 수 있다.
- 트리의 키 값은 보다 큼, 보다 작음을 사용하여 비교 가능
- 트리에서 각 노드의 키 값은 오른쪽 하위 트리의 모든 키 값보다 작고 왼쪽 하위 트리의 모든 키 값보다 크다.
- 바이너리 서치트리인 경우에는 좌측 트리의 값은 우측 트리의 모든 값보다 모두 작다.
- BST인 경우 동일한 데이터가 삽입되더라도 순서가 달라지면 모양이 달라질 수 있다. 즉, 키 값과 삽입 순서 모두에 영향을 받는다.
- 삽입과정은 재귀연산을 통해 진행한다.
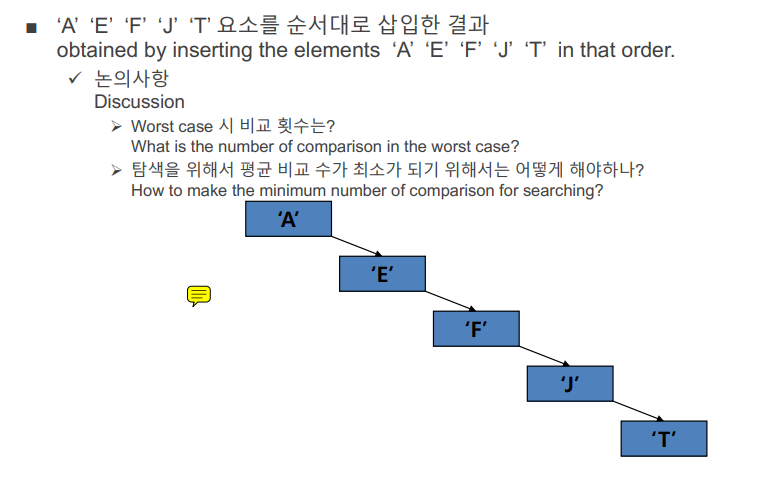
- 동일한 레벨에 있는 노드들은 좌측에 있는 값이 우측에 있는 값보다 작다. 하지만 만약 한 방향의 깊이가 길어질 경우에는 효율이 떨어질 수 밖에 없다. 따라서 데이터 삽입 순서에 따라 트리의 높이랑 모양이 달라진다. 최악의 경우에는 (예제에서는 J보다 더 큰 값을 찾을 때) N번만큼 비교를 하게된다. 이때에는 랜덤하게 3개의 값을 뽑아 그 값들의 중앙값을 기준으로 루트를 설정하면 적당히 밸런스를 유지할 수 있다. 하지만 이러한 경우에도 데이터가 삽입될 때마다 언밸런스하게 될 수 있다. 이를 위해 밸런스를 보장하는 방식이 생겨났다.
- 현재 포인터가 NULL이면 삽입한다? -> insert 함수에서 포인터의 참조변수(*&)를 파라미터로 전달받아서 해더 값에 노드를 추가한다. 레퍼런스가 없으면 할당은 하지만 변경된 내용이 적용되지 않게된다.
- 오름차순으로 데이터를 삽입한 경우 순차탐색과 동일한 시간복잡도를 가지게 된다. 따라서 루트 노드를 무엇으로 잡느냐가 중요하다. 이에 따라 랜덤하게 3개의 값을 뽑아서 그 중간값을 루트로 만들 수 있다.
2) 트리 노드 개수를 센다면?
- 재귀 형태를 이용해 구현하면 깔끔하다.
- Case 1 ~ 3은 틀렸다.
- case1: and로 묶으면 shortcut때문에 우항을 체크하지 않을 수 있다. 이는 partially complete binary tree는 해당이 안되겠지만 BST는 좌항이 없지만 우항이 존재할 수 있기 때문에 우항도 체크해야한다.
- case2: 빈 트리에 대해 호출한다면 이를 처리해줄 수 없다.
- case3: 둘 다 널인 경우에는 1을 반환하는데 그 이후 비어있는 노드에 대해 또 countNode를 호출하여 의미없는 연산을 한다.
3) Delete 구현
- Retrieve 함수와 유사하다.
- 재귀호출에서 시작지점을 지정해주기 위한 wrapper 함수를 동원해서 재귀호출의 시작지점을 잡아주곤 한다.
- 포인터의 레퍼런스를 가져와서 삭제나 이동이 가능하게끔 구현한다.
(1) Leaf node인 경우
- 삭제한다.
- 리프노드는 자식노드가 존재하지 않는 경우가 된다.
(2) 자식 노드가 둘 다 있는 경우
- 좌측 노드 중 가장 오른쪽에 있는 노드를 현재 위치로 옮겨준다. 혹은 우측 노드 중 가장 왼족에 있는 노드를 현재 위치로 옮겨준다. 이에 따라 정렬성이 유지된다. 그렇게 되면 좌측 서브트리 중 가장 큰 값 혹은 우측 서브트리 중 가장 작은 값으로 대체된다.
(3) 자식 노드 중 하나만 있는 경우
- 부모의 포인터를 자기 자신이 가리키고 있는 노드로 바꾼다.
4. Tree의 순회
- 어떤 순서로 노드를 탐색할 것인가.
- 재귀형태로 값을 출력한다.
1) Inorder Traversal
- 트리 내에 있는 값이 작은 값부터 큰 값으로 정렬된 형태로 출력할 수 있다.
- left를 먼저 돌고 이후에 right을 한다. 이때 자식노드의 값이 null일 때까지 갔다가 값을 출력한다.
2) Preorder Traversal
- 탐색하는 것부터 출력하는 식으로 출력한다.
- 자기 자신부터 먼저 출력하고 탐색을 진행한다.
3) Postorder Traversal
- Left 먼저 탐색하고, Right 탐색한 뒤, 자기 자신은 이후에 출력한다.
- cpu가 수식을 처리할 떄 preoreder, postorder를 사용하는 것이 더 유리한 경우가 있다.
cf) 소멸자 구현
- Linked tree는 객체의 소멸 시점에서 이를 제거하지 않으면 메모리 누수가 발생한다. 이를 해결하기 위해서 소멸자를 정의해야한다. 이를 위해 순회에 맞춰하며 삭제해야한다.
- 예제는 post로 순회한다.
- 힙은 부분완전이진트리이지만 BST는 아니다.
'강의 내용 정리 > 자료구조' 카테고리의 다른 글
| 자료구조 (10), Graph (0) | 2022.06.21 |
|---|---|
| 자료구조 (9), Priority Queue (0) | 2022.06.21 |
| 자료구조 (7), 재귀호출 (0) | 2022.06.19 |
| 자료구조 구현 (1), Unsorted list (0) | 2022.05.11 |
| 자료구조 (6), Linked Structured (0) | 2022.05.02 |