2021. 5. 25. 20:35ㆍ알고리즘/그리디
문제 정의
상근이는 요즘 설탕공장에서 설탕을 배달하고 있다. 상근이는 지금 사탕가게에 설탕을 정확하게 N킬로그램을 배달해야 한다. 설탕공장에서 만드는 설탕은 봉지에 담겨져 있다. 봉지는 3킬로그램 봉지와 5킬로그램 봉지가 있다.
상근이는 귀찮기 때문에, 최대한 적은 봉지를 들고 가려고 한다. 예를 들어, 18킬로그램 설탕을 배달해야 할 때, 3킬로그램 봉지 6개를 가져가도 되지만, 5킬로그램 3개와 3킬로그램 1개를 배달하면, 더 적은 개수의 봉지를 배달할 수 있다.
상근이가 설탕을 정확하게 N킬로그램 배달해야 할 때, 봉지 몇 개를 가져가면 되는지 그 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. (3 ≤ N ≤ 5000)
출력
상근이가 배달하는 봉지의 최소 개수를 출력한다. 만약, 정확하게 N킬로그램을 만들 수 없다면 -1을 출력한다.
예제 입력 1
18예제 출력 1
4예제 입력 2
4예제 출력 2
-1예제 입력 3
6예제 출력 3
2예제 입력 4
9예제 출력 4
3예제 입력 5
11예제 출력 5
3
접근 방법 1 (경우의 수에 따른 조건문 사용)
1. 설탕의 무게를 3으로 나눌 경우 최소한의 봉지만으로 배달할 수 없는 경우가 생기기에 설탕 무게를 5로 나눈다.
2. 5로 나눌 때의 나머지가 1 ~ 4일 경우의 경우의 수를 각각 고려해 3과 5로 절대 나눠지지 않는 경우의 수를 고려한다.(이를테면 5로 나눌 때의 나머지가 2인 경우 7은 3과 5의 조합으로 나눌 수 없다. 하지만 12 이상의 숫자는 3과 5의 조합으로 나눌 수 있다.)
3. 각각의 경우의 수를 따져가며 3과 5의 조합으로 나눠지지 않는 경우(5로 나눌 때 나머지가 2인 경우 : 7)와 그 외의 경우들(5로 나눌 때 나머지가 2인 경우 : 12 이상)에 대해 조건문을 사용해 프로그램을 작성한다.
코드
n = int(input())
bag = 0
if n >= 5:
if n % 5 == 0:
bag += n // 5
elif n % 5 == 1:
bag += (n // 5 - 1) + 2
elif n % 5 == 2:
if n // 5 >= 2:
bag += n // 5 + 2
else:
bag = -1
elif n % 5 == 3:
bag += n // 5 + 1
elif n % 5 == 4:
bag += n // 5 - 1 + 3
else:
if n % 3 == 0:
bag += n // 3
else:
bag = -1
print(bag)
접근 방법 2 (재귀적 호출)
1. 설탕의 무게를 3을 뺄 경우 최소한의 봉지만으로 배달할 수 없는 경우가 생기기에 주어진 설탕 무게 n에서 5를 반복적으로 빼고 봉지의 개수를 하나씩 추가한다..
2. 이를 반복적으로 시행하다 n이 특정한 3의 배수(3, 6, 9, 12)가 되었을 때 3으로 나눠준 뒤 종료한다.
코드
n = int(input())
def result(n, bag=0):
if n < 5 and n % 3 != 0:
return -1
elif n % 5 == 0:
return bag+n//5
elif n % 5 == 1 and n == 6:
return bag+2
elif n % 5 == 2 and n == 12:
return bag+4
elif n % 5 == 3:
return bag+n//5+1
elif n % 5 == 4 and n == 9:
return bag+3
else:
return result(n-5, bag+1)
print(result(n))혹은 다음과 같이 풀이할 수 있다.
n = int(input())
def result(n, bag=0):
if n < 5 and n % 3 != 0:
return -1
elif n % 5 == 0:
return bag+n//5
elif n in [3, 6, 9, 12]:
return bag+n//3
else:
return result(n-5, bag+1)
print(result(n))
접근 방식 1과 접근 방식 2의 시간 복잡도 비교
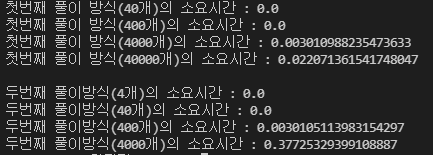
접근 방식 1의 경우, 주어진 값에 대해 몫과 나머지를 통해 바로 값을 도출하는 특징이 있다.
하지만 접근 방식 2의 경우, 주어진 값에 대해 계속해서 특정 값에 도달하기 전까지 5를 빼기 때문에 소요시간이 훨씬 긴 것을 볼 수 있다.
접근 방식 1의 경우 입력변수가 약 10배가 늘었을 때 소요시간은 10배에 조금 못미치는 수준으로 늘었다.
반면 접근 방식 2의 경우 입력변수가 약 10배가 늘었을 때 소요시간은 약 100배이상으로 늘어난 것을 확인할 수 있다.
또한 5000개 이상부터는 RecursionError로 작동하지 않았다.
알고리즘을 공부하고 정리해야겠다는 생각이 들어 백준 온라인 저널에서 처음으로 알고리즘 문제를 풀어봤는데 그리디 알고리즘 중 첫 문제라 그런지 생각보다 어렵지 않았다. 문제를 제출하고 다른 분들의 풀이를 보던 중 재귀적 방식으로 푼 걸 보고 재밌겠다 싶어서 재귀적 방식으로도 한번 코드를 짜봤다. 1일 2 ~ 3문제 정도 꾸준히 풀며 정리할 예정이다.
'알고리즘 > 그리디' 카테고리의 다른 글
| 백준 온라인 저널, 그리디 알고리즘/5585번 : 거스름돈(파이썬) (0) | 2021.06.03 |
|---|---|
| 이코테 2021, 그리디 알고리즘/ 모험가 길드(파이썬) (0) | 2021.06.01 |
| 백준 온라인 저널, 그리디 알고리즘/1931번 : 회의실 배정(파이썬) (0) | 2021.05.31 |
| 백준 온라인 저널, 그리디 알고리즘/11047번 : 동전 0(파이썬) (0) | 2021.05.31 |
| 백준 온라인 저널, 그리디 알고리즘/11399번 : ATM(파이썬) (0) | 2021.05.25 |