문제
홍수의 발생으로 인해 도시의 도로들이 유실되어 많은 ICP(International Computational Plan) 시민들이 불편을 겪고 있다. 도시는 아래와 같은 격자 형태로 표현이 된다고 가정하자. 검정색 단위 격자가 ‘단위도로’를 의미하며 흰색 단위 격자는 도로가 없었거나 유실된 상태를 의미한다. X로 표시된 단위 격자는 도로를 건설할 수 없는 곳을 의미한다.
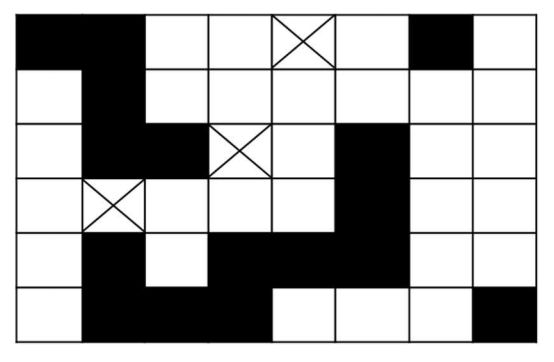
도시의 차들은 단위 도로 상에서 가로나 세로 방향으로만 움직인다고 가정했을 때 도시의 기능을 회복시키기 위해 맨 왼쪽 위 단위 격자에서 맨 오른쪽 아래 단위 격자로 도시의 차들이 가는 경로를 만들기 위해 필요한 최소한의 도로 건설 비용을 계산하고자 한다. 단위 도로 하나를 건설하기 위해 1 또는 2 의 비용이 소요된다고 가정하자. 위 그림에서는 흰색 단위 격자에 단위 도로 하나를 건설하기 위해서는 1 의 비용이 든다고 가정한다.
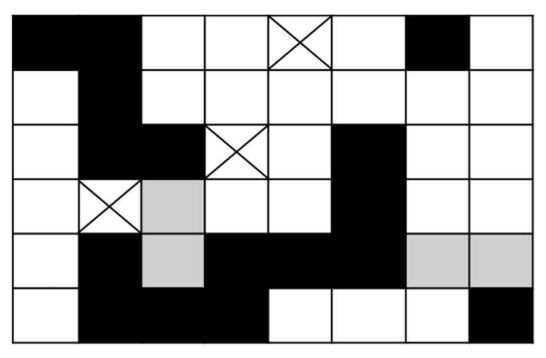
위와 같이 회색으로 표시된 단위 도로들을 4 의 비용으로 건설하면 목적을 달성할 수 있다.
도시가 위와 같이 격자 형태로 주어졌을 때 맨 왼쪽 위 단위 격자에서 맨 오른쪽 아래 단위 격자로 가는 경로를 만들기 위해 필요한 최소 도로 건설 비용을 구하는 프로그램을 작성하시오.
출력
출력은 표준출력을 사용한다. 도시의 맨 왼쪽 위 단위 격자에서 맨 오른쪽 아래 단위 격자로 가는 경로를 만들기 위해 필요한 최소한의 도로 건설 비용을 한 줄에 출력한다. 해당 경로를 건설할 수 없을 때는 -1 을 출력한다.
W3sicHJvYmxlbV9pZCI6IjIwMDQ2IiwicHJvYmxlbV9sYW5nIjoiMCIsInRpdGxlIjoiUm9hZCBSZWNvbnN0cnVjdGlvbiIsImRlc2NyaXB0aW9uIjoiPHA+XHVkNjRkXHVjMjE4XHVjNzU4IFx1YmMxY1x1YzBkZFx1YzczY1x1Yjg1YyBcdWM3NzhcdWQ1NzQgXHViM2M0XHVjMmRjXHVjNzU4IFx1YjNjNFx1Yjg1Y1x1YjRlNFx1Yzc3NCBcdWM3MjBcdWMyZTRcdWI0MThcdWM1YjQgXHViOWNlXHVjNzQwIElDUChJbnRlcm5hdGlvbmFsIENvbXB1dGF0aW9uYWwgUGxhbikgXHVjMmRjXHViYmZjXHViNGU0XHVjNzc0IFx1YmQ4OFx1ZDNiOFx1Yzc0NCBcdWFjYWFcdWFjZTAgXHVjNzg4XHViMmU0LiBcdWIzYzRcdWMyZGNcdWIyOTQgXHVjNTQ0XHViNzk4XHVjNjQwIFx1YWMxOVx1Yzc0MCBcdWFjYTlcdWM3OTAgXHVkNjE1XHVkMGRjXHViODVjIFx1ZDQ1Y1x1ZDYwNFx1Yzc3NCBcdWI0MWNcdWIyZTRcdWFjZTAgXHVhYzAwXHVjODE1XHVkNTU4XHVjNzkwLiBcdWFjODBcdWM4MTVcdWMwYzkgXHViMmU4XHVjNzA0IFx1YWNhOVx1Yzc5MFx1YWMwMCAmbHNxdW87XHViMmU4XHVjNzA0XHViM2M0XHViODVjJnJzcXVvO1x1Yjk3YyBcdWM3NThcdWJiZjhcdWQ1NThcdWJhNzAgXHVkNzcwXHVjMGM5IFx1YjJlOFx1YzcwNCBcdWFjYTlcdWM3OTBcdWIyOTQgXHViM2M0XHViODVjXHVhYzAwIFx1YzVjNlx1YzVjOFx1YWM3MFx1YjA5OCBcdWM3MjBcdWMyZTRcdWI0MWMgXHVjMGMxXHVkMGRjXHViOTdjIFx1Yzc1OFx1YmJmOFx1ZDU1Y1x1YjJlNC4gWFx1Yjg1YyBcdWQ0NWNcdWMyZGNcdWI0MWMgXHViMmU4XHVjNzA0IFx1YWNhOVx1Yzc5MFx1YjI5NCBcdWIzYzRcdWI4NWNcdWI5N2MgXHVhYzc0XHVjMTI0XHVkNTYwIFx1YzIxOCBcdWM1YzZcdWIyOTQgXHVhY2YzXHVjNzQ0IFx1Yzc1OFx1YmJmOFx1ZDU1Y1x1YjJlNC48XC9wPlxyXG5cclxuPHAgc3R5bGU9XCJ0ZXh0LWFsaWduOiBjZW50ZXI7XCI+PGltZyBhbHQ9XCJcIiBzcmM9XCJodHRwczpcL1wvdXBsb2FkLmFjbWljcGMubmV0XC9kZjdkNjVkMS0xZDYwLTQ0NTYtOWM2ZS1hNjgwM2UzMzEwMzlcLy1cL3ByZXZpZXdcL1wiIHN0eWxlPVwid2lkdGg6IDI3N3B4OyBoZWlnaHQ6IDE4MXB4O1wiIFwvPjxcL3A+XHJcblxyXG48cD5cdWIzYzRcdWMyZGNcdWM3NTggXHVjYzI4XHViNGU0XHVjNzQwIFx1YjJlOFx1YzcwNCBcdWIzYzRcdWI4NWMgXHVjMGMxXHVjNWQwXHVjMTFjIFx1YWMwMFx1Yjg1Y1x1YjA5OCBcdWMxMzhcdWI4NWMgXHViYzI5XHVkNWE1XHVjNzNjXHViODVjXHViOWNjIFx1YzZjMFx1YzljMVx1Yzc3OFx1YjJlNFx1YWNlMCBcdWFjMDBcdWM4MTVcdWQ1ODhcdWM3NDQgXHViNTRjIFx1YjNjNFx1YzJkY1x1Yzc1OCBcdWFlMzBcdWIyYTVcdWM3NDQgXHVkNjhjXHViY2Y1XHVjMmRjXHVkMGE0XHVhZTMwIFx1YzcwNFx1ZDU3NCBcdWI5ZTggXHVjNjdjXHVjYWJkIFx1YzcwNCBcdWIyZThcdWM3MDQgXHVhY2E5XHVjNzkwXHVjNWQwXHVjMTFjIFx1YjllOCBcdWM2MjRcdWI5NzhcdWNhYmQgXHVjNTQ0XHViNzk4IFx1YjJlOFx1YzcwNCBcdWFjYTlcdWM3OTBcdWI4NWMgXHViM2M0XHVjMmRjXHVjNzU4IFx1Y2MyOFx1YjRlNFx1Yzc3NCBcdWFjMDBcdWIyOTQgXHVhY2JkXHViODVjXHViOTdjIFx1YjljY1x1YjRlNFx1YWUzMCBcdWM3MDRcdWQ1NzQgXHVkNTQ0XHVjNjk0XHVkNTVjIFx1Y2Q1Y1x1YzE4Y1x1ZDU1Y1x1Yzc1OCBcdWIzYzRcdWI4NWMgXHVhYzc0XHVjMTI0IFx1YmU0NFx1YzZhOVx1Yzc0NCBcdWFjYzRcdWMwYjBcdWQ1NThcdWFjZTBcdWM3OTAgXHVkNTVjXHViMmU0LiBcdWIyZThcdWM3MDQgXHViM2M0XHViODVjIFx1ZDU1OFx1YjA5OFx1Yjk3YyBcdWFjNzRcdWMxMjRcdWQ1NThcdWFlMzAgXHVjNzA0XHVkNTc0IDEgXHViNjEwXHViMjk0IDIgXHVjNzU4IFx1YmU0NFx1YzZhOVx1Yzc3NCBcdWMxOGNcdWM2OTRcdWI0MWNcdWIyZTRcdWFjZTAgXHVhYzAwXHVjODE1XHVkNTU4XHVjNzkwLiBcdWM3MDQgXHVhZGY4XHViOWJjXHVjNWQwXHVjMTFjXHViMjk0IFx1ZDc3MFx1YzBjOSBcdWIyZThcdWM3MDQgXHVhY2E5XHVjNzkwXHVjNWQwIFx1YjJlOFx1YzcwNCBcdWIzYzRcdWI4NWMgXHVkNTU4XHViMDk4XHViOTdjIFx1YWM3NFx1YzEyNFx1ZDU1OFx1YWUzMCBcdWM3MDRcdWQ1NzRcdWMxMWNcdWIyOTQgMSBcdWM3NTggXHViZTQ0XHVjNmE5XHVjNzc0IFx1YjRlMFx1YjJlNFx1YWNlMCBcdWFjMDBcdWM4MTVcdWQ1NWNcdWIyZTQuPFwvcD5cclxuXHJcbjxwIHN0eWxlPVwidGV4dC1hbGlnbjogY2VudGVyO1wiPjxpbWcgYWx0PVwiXCIgc3JjPVwiaHR0cHM6XC9cL3VwbG9hZC5hY21pY3BjLm5ldFwvZDk1MjkyMTUtYWFiZi00YjY1LTg3NWEtOTRiZDY3NTIzODZjXC8tXC9wcmV2aWV3XC9cIiBzdHlsZT1cIndpZHRoOiAyNzNweDsgaGVpZ2h0OiAxNzlweDtcIiBcLz48XC9wPlxyXG5cclxuPHA+XHVjNzA0XHVjNjQwIFx1YWMxOVx1Yzc3NCBcdWQ2OGNcdWMwYzlcdWM3M2NcdWI4NWMgXHVkNDVjXHVjMmRjXHViNDFjIFx1YjJlOFx1YzcwNCBcdWIzYzRcdWI4NWNcdWI0ZTRcdWM3NDQgNCBcdWM3NTggXHViZTQ0XHVjNmE5XHVjNzNjXHViODVjIFx1YWM3NFx1YzEyNFx1ZDU1OFx1YmE3NCBcdWJhYTlcdWM4MDFcdWM3NDQgXHViMmVjXHVjMTMxXHVkNTYwIFx1YzIxOCBcdWM3ODhcdWIyZTQuPFwvcD5cclxuXHJcbjxwPlx1YjNjNFx1YzJkY1x1YWMwMCBcdWM3MDRcdWM2NDAgXHVhYzE5XHVjNzc0IFx1YWNhOVx1Yzc5MCBcdWQ2MTVcdWQwZGNcdWI4NWMgXHVjOGZjXHVjNWI0XHVjODRjXHVjNzQ0IFx1YjU0YyBcdWI5ZTggXHVjNjdjXHVjYWJkIFx1YzcwNCBcdWIyZThcdWM3MDQgXHVhY2E5XHVjNzkwXHVjNWQwXHVjMTFjIFx1YjllOCBcdWM2MjRcdWI5NzhcdWNhYmQgXHVjNTQ0XHViNzk4IFx1YjJlOFx1YzcwNCBcdWFjYTlcdWM3OTBcdWI4NWMgXHVhYzAwXHViMjk0IFx1YWNiZFx1Yjg1Y1x1Yjk3YyBcdWI5Y2NcdWI0ZTRcdWFlMzAgXHVjNzA0XHVkNTc0IFx1ZDU0NFx1YzY5NFx1ZDU1YyBcdWNkNWNcdWMxOGMgXHViM2M0XHViODVjIFx1YWM3NFx1YzEyNCBcdWJlNDRcdWM2YTlcdWM3NDQgXHVhZDZjXHVkNTU4XHViMjk0IFx1ZDUwNFx1Yjg1Y1x1YWRmOFx1YjdhOFx1Yzc0NCBcdWM3OTFcdWMxMzFcdWQ1NThcdWMyZGNcdWM2MjQuPFwvcD5cclxuIiwiaW5wdXQiOiI8cD5cdWM3ODVcdWI4MjVcdWM3NDAgXHVkNDVjXHVjOTAwXHVjNzg1XHViODI1XHVjNzQ0IFx1YzBhY1x1YzZhOVx1ZDU1Y1x1YjJlNC4gXHVjY2FiIFx1YmM4OFx1YzlmOCBcdWM5MDRcdWM1ZDAgXHViM2M0XHVjMmRjXHViOTdjIFx1ZDQ1Y1x1ZDYwNFx1ZDU1OFx1YjI5NCBcdWFjYTlcdWM3OTBcdWM3NTggXHVkNTg5XHVhY2ZjIFx1YzVmNFx1Yzc1OCBcdWQwNmNcdWFlMzBcdWI5N2MgXHVhYzAxXHVhYzAxIFx1YjA5OFx1ZDBjMFx1YjBiNFx1YjI5NCBcdWI0NTAgXHVhYzFjXHVjNzU4IFx1YzU5MVx1Yzc1OCBcdWM4MTVcdWMyMTggPGVtPm08XC9lbT4sIDxlbT5uPFwvZW0+ICgxICZsZTsgPGVtPm08XC9lbT4sIDxlbT5uPFwvZW0+ICZsZTsgMSwwMDAsIDEgJmx0OyBtJnRpbWVzO24pXHVjNzc0IFx1YzhmY1x1YzViNFx1YzljNFx1YjJlNC4gXHViMmU0XHVjNzRjIDxlbT5tPFwvZW0+XHVhYzFjXHVjNzU4IFx1YWMwMSBcdWM5MDRcdWM1ZDAgXHVhY2E5XHVjNzkwXHVjNzU4IFx1YWMwMSBcdWM1ZjRcdWM3NTggXHVjODE1XHViY2Y0XHViOTdjIFx1YjA5OFx1ZDBjMFx1YjBiNFx1YjI5NCA8ZW0+bjxcL2VtPlx1YWMxY1x1Yzc1OCBcdWMyMmJcdWM3OTBcdWFjMDAgXHVjOGZjXHVjNWI0XHVjOWM0XHViMmU0LiBcdWFjMDEgXHVjNWY0XHVjNzU4IFx1YzgxNVx1YmNmNFx1YjI5NCBcdWM4MTVcdWMyMTggMCwgMSwgMiwgLTEgXHViODVjIFx1YjA5OFx1ZDBjMFx1YjBiNFx1YmE3MCAwIFx1Yzc0MCBcdWIyZThcdWM3MDRcdWIzYzRcdWI4NWNcdWFjMDAgXHVjNzc0XHViYmY4IFx1Yzg3NFx1YzdhY1x1ZDU1OFx1YjI5NCBcdWFjODNcdWM3NDQsIFx1Yzk4OSwgXHViM2M0XHViODVjXHVjNWQwIFx1YzcyMFx1YzJlNFx1Yzc3NCBcdWM1YzZcdWIyOTQgXHVjMGMxXHVkMGRjLCAxIFx1Yzc0MCBcdWIyZThcdWM3MDQgXHViM2M0XHViODVjXHVhYzAwIFx1YzVjNlx1YWNlMCAxIFx1Yzc1OCBcdWJlNDRcdWM2YTlcdWM3M2NcdWI4NWMgXHViM2M0XHViODVjXHViOTdjIFx1YWM3NFx1YzEyNFx1ZDU2MCBcdWMyMTggXHVjNzg4XHViMjk0IFx1YjJlOFx1YzcwNCBcdWFjYTlcdWM3OTAsIDIgXHViMjk0IFx1YjJlOFx1YzcwNCBcdWIzYzRcdWI4NWNcdWFjMDAgXHVjNWM2XHVhY2UwIDIgXHVjNzU4IFx1YmU0NFx1YzZhOVx1YzczY1x1Yjg1YyBcdWIzYzRcdWI4NWNcdWI5N2MgXHVhYzc0XHVjMTI0XHVkNTYwIFx1YzIxOCBcdWM3ODhcdWIyOTQgXHViMmU4XHVjNzA0IFx1YWNhOVx1Yzc5MFx1Yjk3YyBcdWM3NThcdWJiZjhcdWQ1NWNcdWIyZTQuIC0xIFx1Yzc0MCBYXHViODVjIFx1ZDQ1Y1x1YzJkY1x1YjQxYyBcdWIyZThcdWM3MDQgXHVhY2E5XHVjNzkwXHViODVjIFx1YWRmOCBcdWM3MDRcdWNlNThcdWM1ZDAgXHViMmU4XHVjNzA0IFx1YjNjNFx1Yjg1Y1x1Yjk3YyBcdWFjNzRcdWMxMjRcdWQ1NjAgXHVjMjE4IFx1YzVjNlx1YjI5NCBcdWMwYzFcdWQwZGNcdWI5N2MgXHVjNzU4XHViYmY4XHVkNTVjXHViMmU0LjxcL3A+XHJcbiIsIm91dHB1dCI6IjxwPlx1Y2Q5Y1x1YjgyNVx1Yzc0MCBcdWQ0NWNcdWM5MDBcdWNkOWNcdWI4MjVcdWM3NDQgXHVjMGFjXHVjNmE5XHVkNTVjXHViMmU0LiBcdWIzYzRcdWMyZGNcdWM3NTggXHViOWU4IFx1YzY3Y1x1Y2FiZCBcdWM3MDQgXHViMmU4XHVjNzA0IFx1YWNhOVx1Yzc5MFx1YzVkMFx1YzExYyBcdWI5ZTggXHVjNjI0XHViOTc4XHVjYWJkIFx1YzU0NFx1Yjc5OCBcdWIyZThcdWM3MDQgXHVhY2E5XHVjNzkwXHViODVjIFx1YWMwMFx1YjI5NCBcdWFjYmRcdWI4NWNcdWI5N2MgXHViOWNjXHViNGU0XHVhZTMwIFx1YzcwNFx1ZDU3NCBcdWQ1NDRcdWM2OTRcdWQ1NWMgXHVjZDVjXHVjMThjXHVkNTVjXHVjNzU4IFx1YjNjNFx1Yjg1YyBcdWFjNzRcdWMxMjQgXHViZTQ0XHVjNmE5XHVjNzQ0IFx1ZDU1YyBcdWM5MDRcdWM1ZDAgXHVjZDljXHViODI1XHVkNTVjXHViMmU0LiBcdWQ1NzRcdWIyZjkgXHVhY2JkXHViODVjXHViOTdjIFx1YWM3NFx1YzEyNFx1ZDU2MCBcdWMyMTggXHVjNWM2XHVjNzQ0IFx1YjU0Y1x1YjI5NCAtMSBcdWM3NDQgXHVjZDljXHViODI1XHVkNTVjXHViMmU0LjxcL3A+XHJcbiIsImhpbnQiOiIiLCJvcmlnaW5hbCI6IjEiLCJodG1sX3RpdGxlIjoiMCIsInByb2JsZW1fbGFuZ190Y29kZSI6IktvcmVhbiJ9LHsicHJvYmxlbV9pZCI6IjIwMDQ2IiwicHJvYmxlbV9sYW5nIjoiMSIsInRpdGxlIjoiUm9hZCBSZWNvbnN0cnVjdGlvbiIsImRlc2NyaXB0aW9uIjoiPHA+SUNQKEludGVybmF0aW9uYWwgQ29tcHV0YXRpb25hbCBQbGFuKSBDaXR5IGlzIGZhY2VkIHdpdGggbmF0dXJhbCBkaXNhc3RlciwgZmxvb2RpbmcuIEEgbG90IG9mIGl0cyB0cmFuc3BvcnRhdGlvbiByb2FkcyBhcmUgZGVzdHJ1Y3RlZCBiZWNhdXNlIG9mIHRoZSBmbG9vZGluZy4gVGhlIGNpdHkgaXMgcGxhbm5pbmcgdG8gcmVjb25zdHJ1Y3QgaXRzIHJvYWRzLiBUbyBzaW1wbGlmeSB0aGUgcHJvYmxlbSwgdGhlIGNpdHkgaXMgcmVwcmVzZW50ZWQgYnkgYSBncmlkIHN0cnVjdHVyZSBsaWtlIHRoZSBmb2xsb3dpbmcgZmlndXJlLiBXZSBjYWxsIGl0IGFzIGNpdHkgZ3JpZC4gQSB1bml0IGdyaWQgY2VsbCB3aXRoIGJsYWNrIGNvbG9yIG1lYW5zIGEgdW5pdCByb2FkLiBBIHVuaXQgZ3JpZCBjZWxsIHdpdGggd2hpdGUgY29sb3IgbWVhbnMgYW4gYXJlYSB3aGVyZSBhIHVuaXQgcm9hZCBpcyBkZXN0cnVjdGVkIG9yIHdoZXJlIGEgdW5pdCByb2FkIGhhcyBub3QgZXhpc3RlZCBwcmV2aW91c2x5LiBBIHVuaXQgZ3JpZCBjZWxsIHdpdGggWCBkZW5vdGVzIGFuIGFyZWEgd2hlcmUgYSByb2FkIGNhbm5vdCBiZSBjb25zdHJ1Y3RlZC48XC9wPlxyXG5cclxuPHAgc3R5bGU9XCJ0ZXh0LWFsaWduOiBjZW50ZXI7XCI+PGltZyBhbHQ9XCJcIiBzcmM9XCJodHRwczpcL1wvdXBsb2FkLmFjbWljcGMubmV0XC9kZjdkNjVkMS0xZDYwLTQ0NTYtOWM2ZS1hNjgwM2UzMzEwMzlcLy1cL3ByZXZpZXdcL1wiIHN0eWxlPVwid2lkdGg6IDI3N3B4OyBoZWlnaHQ6IDE4MXB4O1wiIFwvPjxcL3A+XHJcblxyXG48cD5XZSBhc3N1bWUgdGhhdCBjYXJzIGluIHRoZSBjaXR5IGNhbiBnbyBob3Jpem9udGFsbHkgb3IgdmVydGljYWxseSBmcm9tIGEgYmxhY2sgY29sb3JlZCBjZWxsIHRvIGFuIGFkamFjZW50IGJsYWNrIGNvbG9yZWQgY2VsbC4gRm9yIHR3byBncmlkIGNlbGxzIDxlbT51PFwvZW0+IGFuZCA8ZW0+djxcL2VtPiBpbiB0aGUgY2l0eSBncmlkLCBpZiBhIGNhciBjYW4gZ28gZnJvbSA8ZW0+dTxcL2VtPiB0byA8ZW0+djxcL2VtPiBhbmQgdGhlIGJvdGggY2VsbHMgYXJlIGJsYWNrIGNvbG9yZWQsIHRoZW4gPGVtPnU8XC9lbT4gYW5kIDxlbT52PFwvZW0+IGFyZSBjYWxsZWQgPGVtPmNvbm5lY3RlZDxcL2VtPi4gSUNQIGNpdHkgaXMgcGxhbm5pbmcgdG8gcmVjb25zdHJ1Y3QgaXRzIHRyYW5zcG9ydGF0aW9uIHJvYWRzIGJ5IGNvbm5lY3RpbmcgZ3JpZCBjZWxscyBmcm9tIHRoZSB1cHBlciBhbmQgbGVmdG1vc3QgZ3JpZCB0byB0aGUgbG93ZXIgYW5kIHJpZ2h0bW9zdCBvbmUgd2l0aCBtaW5pbXVtIGNvbnN0cnVjdGlvbiBjb3N0LiBXZSBhc3N1bWUgdGhhdCBpdCBjb3N0cyAxIG9yIDIgZm9yIGNvbnN0cnVjdGluZyBhIHVuaXQgcm9hZC4gRm9yIHRoZSBleGFtcGxlIGFib3ZlLCB0aGUgZ3JheSBjZWxscyBpbiB0aGUgZm9sbG93aW5nIGZpZ3VyZSBzaG93IGhvdyB0byBjb25zdHJ1Y3Qgcm9hZHMgdGhhdCBjb25uZWN0IHRoZSB1cHBlciBhbmQgbGVmdG1vc3QgZ3JpZCBjZWxsIHdpdGggdGhlIGxvd2VyIGFuZCByaWdodG1vc3Qgb25lIGJ5IHRoZSBtaW5pbXVtIGNvbnN0cnVjdGlvbiBjb3N0IDQuIFdlIGFzc3VtZSB0aGF0IGl0IGNvc3RzIDEgZm9yIGNvbnN0cnVjdGluZyBhIHVuaXQgcm9hZCBvbiB0aGUgd2hpdGUgY2VsbHMgaW4gdGhlIGZpZ3VyZS4gTm90ZSB0aGF0IGl0IGNvc3RzIDEgb3IgMiBmb3IgY29uc3RydWN0aW5nIGEgdW5pdCByb2FkIGluIGdlbmVyYWwgY2FzZS48XC9wPlxyXG5cclxuPHAgc3R5bGU9XCJ0ZXh0LWFsaWduOiBjZW50ZXI7XCI+PGltZyBhbHQ9XCJcIiBzcmM9XCJodHRwczpcL1wvdXBsb2FkLmFjbWljcGMubmV0XC9kOTUyOTIxNS1hYWJmLTRiNjUtODc1YS05NGJkNjc1MjM4NmNcLy1cL3ByZXZpZXdcL1wiIHN0eWxlPVwid2lkdGg6IDI3M3B4OyBoZWlnaHQ6IDE3OXB4O1wiIFwvPjxcL3A+XHJcblxyXG48cD5HaXZlbiBhIGNpdHkgZ3JpZCwgd3JpdGUgYSBwcm9ncmFtIHRvIGNvbXB1dGUgdGhlIG1pbmltdW0gY29uc3RydWN0aW9uIGNvc3QgdGhhdCBjb25uZWN0cyByb2FkcyBmcm9tIHRoZSB1cHBlciBhbmQgbGVmdG1vc3QgZ3JpZCBjZWxsIHRvIHRoZSBsb3dlciBhbmQgcmlnaHRtb3N0IG9uZS48XC9wPlxyXG4iLCJpbnB1dCI6IjxwPllvdXIgcHJvZ3JhbSBpcyB0byByZWFkIGZyb20gc3RhbmRhcmQgaW5wdXQuIFRoZSBpbnB1dCBzdGFydHMgd2l0aCBhIGxpbmUgY29udGFpbmluZyB0d28gaW50ZWdlcnMsIDxlbT5tPFwvZW0+IGFuZCA8ZW0+bjxcL2VtPiAoMSAmbGU7IDxlbT5tPFwvZW0+ICZsZTsgMSwwMDAsIDEgJmxlOyA8ZW0+bjxcL2VtPiAmbGU7IDEsMDAwKSwgd2hlcmUgPGVtPm08XC9lbT4gYW5kIDxlbT5uPFwvZW0+IGRlbm90ZSB0aGUgbnVtYmVycyBvZiByb3dzIGFuZCBjb2x1bW5zIG9mIHRoZSBncmlkIHRoYXQgcmVwcmVzZW50IHRoZSBjaXR5LCByZXNwZWN0aXZlbHkuIEluIHRoZSBmb2xsb3dpbmcgPGVtPm08XC9lbT4gbGluZXMsIHRoZSA8ZW0+aTxcL2VtPi10aCBsaW5lIGNvbnRhaW5zIDxlbT5uPFwvZW0+IGludGVnZXJzIHRoYXQgcmVwcmVzZW50IHN0YXRlcyBvZiB1bml0IGdyaWQgY2VsbHMgaW4gdGhlIDxlbT5pPFwvZW0+LXRoIHJvdyBvZiB0aGUgY2l0eSBncmlkLiBFYWNoIHN0YXRlIGlzIHJlcHJlc2VudGVkIGJ5IHVzaW5nIGZvdXIgbnVtYmVycyAwLCAxLCAyLCBhbmQgLTEuIFRoZSBudW1iZXIgMCBpbmRpY2F0ZXMgdGhhdCB0aGUgY3VycmVudCB1bml0IGdyaWQgY2VsbCBpcyBhIHVuaXQgcm9hZCwgdGhhdCBpcywgYW4gdW5kYW1hZ2VkIHJvYWQuIFRoZSBudW1iZXJzIDEgYW5kIDIgaW5kaWNhdGUgdGhhdCB0aGUgY3VycmVudCB1bml0IGdyaWQgY2VsbCBpcyBlbXB0eSBhbmQgYSB1bml0IHJvYWQgaXMgY29uc3RydWN0aWJsZSB3aXRoIHRoZSBjb3N0cyAxIGFuZCAyLCByZXNwZWN0aXZlbHkuIFRoZSBudW1iZXIgLTEgaW5kaWNhdGVzIHRoYXQgdGhlIGN1cnJlbnQgdW5pdCBncmlkIGNlbGwgY2Fubm90IGJlIHVzZWQgZm9yIGNvbnN0cnVjdGluZyBhIHJvYWQuPFwvcD5cclxuIiwib3V0cHV0IjoiPHA+WW91ciBwcm9ncmFtIGlzIHRvIHdyaXRlIHRvIHN0YW5kYXJkIG91dHB1dC4gUHJpbnQgZXhhY3RseSBvbmUgbGluZS4gVGhlIGxpbmUgc2hvdWxkIGNvbnRhaW4gdGhlIG1pbmltdW0gY29uc3RydWN0aW9uIGNvc3QgdGhhdCBjb25uZWN0cyByb2FkcyBmcm9tIHRoZSB1cHBlciBhbmQgbGVmdG1vc3QgdW5pdCBncmlkIGNlbGwgdG8gdGhlIGxvd2VyIGFuZCByaWdodG1vc3QgdW5pdCBvbmUuIFdoZW4gaXQgaXMgaW1wb3NzaWJsZSB0byBjb25uZWN0IHJvYWRzIGZyb20gdGhlIHVwcGVyIGFuZCBsZWZ0bW9zdCB1bml0IGdyaWQgY2VsbCB0byB0aGUgbG93ZXIgYW5kIHJpZ2h0bW9zdCBvbmUsIHRoZSBwcm9ncmFtIHNob3VsZCBwcmludCBvdXQgLTEgb24gdGhlIGxpbmUuPFwvcD5cclxuIiwiaGludCI6IiIsIm9yaWdpbmFsIjoiMCIsImh0bWxfdGl0bGUiOiIwIiwicHJvYmxlbV9sYW5nX3Rjb2RlIjoiRW5nbGlzaCJ9XQ==
접근 방법
- 다익스트라 최단경로 알고리즘을 활용해 값을 갱신한다.
코드
# https://www.acmicpc.net/problem/20046
# 접근 방법
# 다익스트라 최단경로 알고리즘을 활용해 값을 갱신한다.
def dijkstra(r, c):
if road[r][c] == -1:
return
cost[r][c] = road[r][c]
q = []
heapq.heappush(q, [cost[r][c], r, c])
while q:
co, r, c = heapq.heappop(q)
if cost[r][c] < co:
continue
for dr, dc in [[1, 0], [-1, 0], [0, 1], [0, -1]]:
if 0<=r+dr <= n-1 and 0<= c+dc<= m-1 and road[r+dr][c+dc] != -1 and cost[r+dr][c+dc] > co + road[r+dr][c+dc]:
cost[r+dr][c+dc] = co + road[r+dr][c+dc]
heapq.heappush(q, [cost[r+dr][c+dc], r+dr, c+dc])
import sys, heapq
input = sys.stdin.readline
n, m = map(int, input().split())
road = [list(map(int, input().split())) for _ in range(n)]
INF = int(1e9)
cost = [[INF for _ in range(m)] for _ in range(n)]
dijkstra(0, 0)
if cost[n-1][m-1] == INF:
print(-1)
else:
print(cost[n-1][m-1])