2021. 1. 6. 17:42ㆍEnglish/Machine learning algorithm
Decision trees are named because they are like trees in the form of class classification through certain criteria.
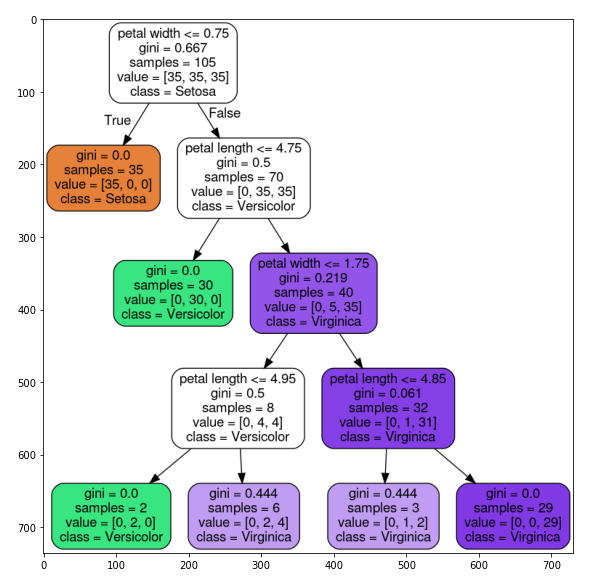
The criteria for classifying decision trees are information gain. Information gains can be determined based on impurity. As the name suggests, impurity is an indicator of how various classes are mixed into the node.
\( IG(D_p,f) = I(D_p) - \sum_{j=1}^{m}\frac{N_j}{N_p}I(D_j) \)
Information gain
f : Characteristics to use for classification
\(D_p\), \(D_j\) : Datasets for parents and jth child nodes
I : Impurity indicator
\(N_p\) : Number of samples on the parent node
\(N_j\) : Number of samples in the jth child node
Simply put, the information gain is determined by the sum of the impurity of the child nodes and the difference between the parent nodes. The lower the impurity of the child nodes, the greater the information gain.
The frequently used indicators of impurity in decision trees are Entropy, Gini impurity, and Classification error.
Entropy
\( I_H(t) = -\sum_{i=1}^{c}P(i|t)log_2P(i|t) \)
Entropy
P(i|t) : Percentage of samples on a specific node t that belong to class i
If the class distribution is even, entropy is maximum. For example, for binary classes, if P(i=1|t) = 1 or P(i=0|t) = 0, the entropy will be zero. Conversely, if P(i=1|t) = 0.5 and P(i=0|t) = 0.5 the entropy is 1. Entropy conditions can be understood as maximizing interdependent information in the tree.
Gini impurity
\( I_G(t) = \sum_{i=1}^{c}P(i|t)(1-P(i|t)) = 1 - \sum_{i=1}^{c}(P(i|t))^2 \)
Gini impurity
Genie impurity can be understood as a criterion for minimizing the probability of misclassification. Like entropy, classes are maximized when they are perfectly mixed. When P(i=1|t) = 0.5 and P(i=0|t) = 0.5, Gini impurity has a value of 0.5.
Classification error
\( I_E = 1 - max(p(i|t)) \)
Classification error
Classification error can be used as a good criterion for pruning, but it is rarely used to construct decision trees due to its disadvantages of being less sensitive to class probability changes.
Binary Classification Scenarios by Indicators of Impurity

\( IG(D_p,f) = I(D_p) - \sum_{j=1}^{m}\frac{N_j}{N_p}I(D_j) \)
Information gain
\( IG(D_p,f) = I(D_p) -\frac{N_{left}}{N_pI(D_{left})} -\frac{N_{right}}{N_p}I(D_{right}) \)
Infomation gain in binary classification
Information gain when using Entropy
\( I_H(t) = -\sum_{i=1}^{c}P(i|t)log_2P(i|t) \)
entropy
$$ I_H(Dp) = -(0.5log_2(0.5) + 0.5log_2(0.5)) = 1$$
$$ A : I_H(D_{left}) = -(\frac{3}{4}log_2(\frac{3}{4}) + \frac{1}{4}log_2(\frac{1}{4}))= 0.81 $$
$$ A : I_H(D_{right}) = -(\frac{1}{4}log_2(\frac{1}{4}) + \frac{3}{4}log_2(\frac{3}{4}))= 0.81 $$
$$ A : IG_H = 1 - \frac{4}{8}0.81 - \frac{4}{8}0.81 = 0.19 $$
$$ B : I_H(D_{left}) = -(\frac{2}{6}log_2(\frac{2}{6}) + \frac{4}{6}log_2(\frac{4}{6}))= 0.92 $$
$$ B : I_H(D_{right}) = 0 $$
$$ B : IG_H = 1 - \frac{6}{8}0.92 - \frac{2}{8}0 = 0.31 $$
We can see that scenario B(\(IG_H = 0.31\)) has higher information gains than scenario A(\(IG_H = 0.19\)). Therefore, it can be seen that B is preferred in the entropy baseline.
Information gain when using Gini impurity
\( I_G(t) = \sum_{i=1}^{c}P(i|t)(1-P(i|t)) = 1 - \sum_{i=1}^{c}(P(i|t))^2 \)
Gini impurity
$$ I_G(D_p) = 1 - (0.5^2 + 0.5^2) = 0.5 $$
$$ A : I_G(D_{left}) = 1 - ((\frac{3}{4})^2 + (\frac{1}{4})^2) = 0.375 $$
$$ A : I_G(D_{right}) = 1 - ((\frac{1}{4})^2 + (\frac{3}{4})^2) = 0.375 $$
$$ A : IG_G = 0.5-\frac{4}{8}0.375 - \frac{4}{8}0.375 = 0.125 $$
$$ B : I_G(D_{left}) = 1 - ((\frac{2}{6})^2 + (\frac{4}{6})^2) = \frac{4}{9} $$
$$ B : I_G(D_{right}) = 0 $$
$$ B : IG_G = 0.5-\frac{6}{8}\frac{4}{9}- 0 = 0.16xx $$
We can see that scenario B(\(IG_G = 0.16xx\)) has higher information gains than scenario A(\(IG_G = 0.125\)). Therefore, we can see that the Gini impurity also favors B.
Information gain when using Classification error
\( I_E = 1 - max(p(i|t)) \)
Classification error
$$ I_E(D_p) = 1 - 0.5 = 0.5 $$
$$ A : I_E(D_{left}) = 1 - \frac{3}{4} = 0.25 $$
$$ A : I_E(D_{right}) = 1 - \frac{3}{4} = 0.25 $$
$$ A : IG_E = 0.5-\frac{4}{8}0.25 - \frac{4}{8}0.25 = 0.25 $$
$$ B : I_E(D_{left}) = 1 - \frac{4}{6} = \frac{1}{3} $$
$$ B : I_E(D_{right}) = 1 - \frac{2}{2} = 0 $$
$$ B : IG_E = 0.5-\frac{6}{8}\frac{1}{3} - \frac{2}{8}0 = 0.25 $$
Scenario B(\(IG_E = 0.25\)) has the same information gains as Scenario A(\(IG_E = 0.25\)) when using the classification error.
Impurity Criteria Comparison
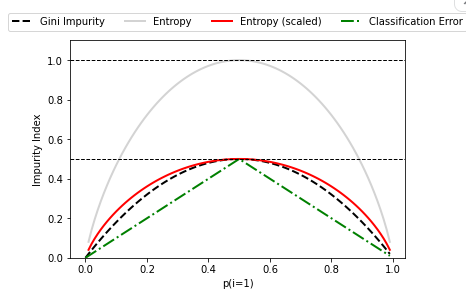
In fact, both genie impurity and entropy produce similar results. The 'scaled' multiplied by 0.5 of entropy shows that it is very similar to Gini impurity. It is better to conduct hyperparameter tuning by changing the level of pruning than to evaluate the tree by changing the impurity conditions.
This can be said to be a splitting condition because the information benefit is determined by the corresponding impurity indicator. Due to these classification conditions, the decision tree repeats this classfication task on all child nodes until the leaf node is pure. However, if the maximum depth of the tree is not limited, it is likely to be overfitting, so we proceed with pruning.
'English > Machine learning algorithm' 카테고리의 다른 글
| [8] Understanding K-Neighborhood (KNN) (0) | 2021.01.17 |
|---|---|
| [7] About RandomForest (0) | 2021.01.07 |
| [5] Non-linear Troubleshooting with Kernel SVM (0) | 2021.01.04 |
| [4] Understand Support Vector Machine (SVM) Principles (linear) (0) | 2020.12.31 |
| [3] Logistic Regression Principles (0) | 2020.12.31 |