2020. 12. 19. 21:33ㆍMathematics(수학)/Linear algebra(선형대수학)
참고 : K-Mooc, Mathematical Fundamentals for Data Science. 고려대학교
데이터 분석을 하기 위해선 기초적인 통계나 수학적인 지식이 필요하죠. 저는 경영학과 출신이기 때문에 경영통계나 경영 수학과 같은 수업은 수강했지만 아직 논문을 읽고 이해할 수 있는 수준이 아니라고 생각해 방학 동안 수학 공부를 하기로 결심했습니다. K-MOOC의 강의를 활용해서 무료 강의를 수강하고 있지만 교수님들께서 직접 해주시는 강의라 그런지 강의 퀄리티는 좋더라고요. K-MOOC 외에도 Coursera와 같은 사이트도 있으니 참고하셔서 듣고 싶은 강의를 찾아보시는 것도 좋을 것 같아요! 저는 현재 Mathematical Funndamentals for Data science라는 강의를 듣고 있고, 강의를 통해 배운 내용을 정리하고자 합니다.
1. 개념
Scalar : a single number
Vector : an ordered list of numbers
Matrix : a two-dimensional array of numbers
간단하게 이해를 돕자면 Vector는 방향과 크기를 나타낸다고 생각하시면 되고 Scalar는 여기에 곱해지거나 나눠질 수 있는 실수라고 생각하시면 됩니다. Vector는 R의 n승에 속한다고 표현하는데 여기서 n은 벡터의 차원이라고 생각하시면 이해하기가 쉬우실 겁니다.

즉, 다음과 같이 표현할 수 있고 벡터는 3차원의 공간 벡터라고 생각하시면 될 것 같습니다.
그리고 이러한 벡터들의 결합이 Matrix라고 할 수 있는데 이 때 행과 열의 개념이 등장해요. horizontal vector는 Row vector라고 지칭하고 vertical vector은 Column vector라고 지칭해요. 위와 같이 Matrix는 R로 표현하는데 행과 열의 곱으로 표현합니다. 만약 Matrix size가 3개의 rows와 2개의 columns를 가지고 있다면 R의 (3 x 2) 제곱으로 표현하는 것이죠.
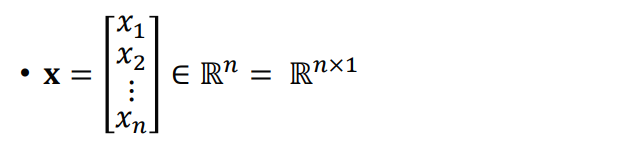
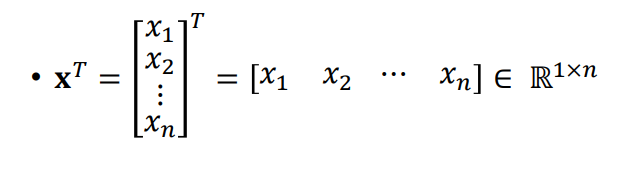
위에 있는 식과 같이 column vector만 존재하는 경우 n개의 rows와 1개의 column만이 존재하기 때문에 해당 식은 R의 N x 1로 표현합니다. 반면 아래와 같이 T라는 기호가 붙게되면 column vector를 row vector로 모양이 바뀌게 됩니다. 그러면 1개의 row와 n개의 columns가 존재하게 되니 이는 1 x N으로 표현할 수 있겠죠.
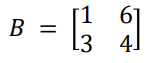
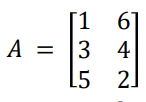
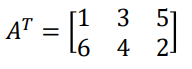
Matrix의 row와 column이 같은 경우 Square matrix, 다른 경우에는 Rectangular matrix라고 지칭하는데 이는 matrix의 모양을 통해서도 직관적으로 알 수 있겠죠.

Matrix의 component를 지칭할 때는 다음과 같이 i행과 j열로 표현해요. 가령 A matrix에서 i = 2, j = 1은 '3'이 되는 것이죠.
2. 연산
Matrix 간의 덧셈은 각각의 같은 행과 열에 해당하는 값들끼리 더해주면 됩니다. 때문에 덧셈을 하게되는 Matrix와 결과로써 나오게 되는 Matrix의 size는 같을 수밖에 없습니다. Scalar를 곱해주는 것도 비슷하게 각 component와 scalar를 곱해주면 됩니다. 여기까지는 직관적으로 생각하는 덧셈과 곱셈의 원리와 같습니다.
반면 Matrix 간의 곱셈은 약간 다릅니다. 왼쪽에서 곱하는 Matrix의 row와 오른쪽에서 곱하는 Matrix의 column간의 조합으로 하나의 component가 만들어지죠.

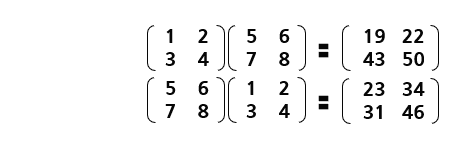
위의 식을 예로 들었을 때 A(1,1)인 1과 B(1,1)인 1을 곱하고, 이를 A(1,2)인 6과 B(2,1)인 2를 서로 곱한 값과 더해줍니다. 식으로 표현하자면 '(A(1,1) x B(1,1)) + (A(1,2) x B(2,1)) = C(1,1) => (1 x 1) + (6 x 2) = 13'이 되는 것이죠. 다른 component 또한 위와 같은 방식으로 곱해줍니다. 다소 복잡해 보이는 식이지만 이로 인해 Matrix의 연산과 관련된 몇 가지 특징을 알 수 있습니다.
우선 왼쪽에 있는 A의 row와 오른쪽에 있는 B의 column간의 조합으로 output이 나오기 때문에 A의 column과 B의 row의 크기가 같아야 합니다. 만약 크기가 다르다면 연산 자체가 불가능합니다. 또한 A의 row와 B의 column의 크기로 Matrix의 크기가 결정됩니다.
A의 크기는 (3 x 2), B의 크기는 (2 x 2)이죠. Matrix의 크기만 확인했을 때 (3 x 2)(2 x 2) = 3 x 2인 것을 확인할 수 있습니다.
또한 Matrix에서는 AB = BA가 성립될 수 없습니다. 두 Matrix의 크기가 다른 경우에는 연산 자체가 불가능하고 Matrix의 위치에 따라 row를 기준으로 곱하느냐, column을 기준으로 곱하느냐가 달라지기 때문입니다.
그밖에도 분배 법칙(Distributive : 'A(B+C) = AB + AC')이나 결합 법칙(Associative : 'A(BC) = (AB)C')이 존재한다. 또한 행렬에서의 Property of transpose이 있다.
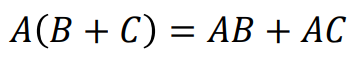
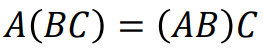

Property of transpose의 경우 Matrix의 크기만 고려해보자. i개의 행과 j개의 열로 구성되어있는 A matrix와 n개의 행과 m개의 열로 구성되어있는 B matrix가 있다고 가정한다면 AB의 크기는 (i x m)이다. 이를 transpose 하게 되면 (m x i)로 이루어진 matrix가 나온다. 우변에서는 B의 transpose 된 (m x n)과 A의 transpose 된 (j x i)를 곱하는 것이기에 (m x i)로 이루어진 matrix가 나온다는 것을 알 수 있다.
'Mathematics(수학) > Linear algebra(선형대수학)' 카테고리의 다른 글
| 선형대수학 2-2. 부분집합 (0) | 2020.12.22 |
|---|---|
| 선형대수학 2-1. 선형 독립 (0) | 2020.12.22 |
| 선형대수학 1-3. 선형조합 (0) | 2020.12.21 |
| 선형대수학 1-2. 선형방정식 (0) | 2020.12.20 |