2020. 12. 21. 17:47ㆍMathematics(수학)/Linear algebra(선형대수학)
참고 : K-Mooc, Mathematical Fundamentals for Data Science. 고려대학교
이전 포스팅에서 선형 회귀와 선형 방정식에 대해서 알아보았습니다.
1-1. Basics Elements of Linear Algebra(선형 회귀의 기본 구성요소)
참고 : K-Mooc, Mathematical Fundamentals for Data Science. 고려대학교 데이터 분석을 하기 위해선 기초적인 통계나 수학적인 지식이 필요하죠. 저는 경영학과 출신이기 때문에 경영통계나 경영 수학과 같은
konghana01.tistory.com
2020/12/20 - [Mathematics(수학)/Linear algebra(선형대수학)] - 1-2. Linear Equation(선형방정식)
1-2. Linear Equation(선형방정식)
참고 : K-Mooc, Mathematical Fundamentals for Data Science. 고려대학교 지난 포스팅에서 선형 회귀의 기본 개념에 대해서 정리했습니다. 오늘은 해당 개념들이 현실에서 어떤 식으로 사용되는지 선형 방정식
konghana01.tistory.com
이번 포스팅에서는 이전 포스팅에서 다루었던 문제를 Linear combination으로 해결해보려 합니다.
1. Linear combination
Linear combination : Vector의 각 항에 특정한 Scalar를 곱하고 더한 것.

여기서 coefficients(계수)는 weights(가중치)라고도 표현하기도 하는데 0을 포함한 모든 실수가 가능해요. 이전 포스팅에서 예시로 들었던 표를 들고 한번 확인해볼게요.

위의 표를 matrix로 표현할 때 다음과 같이 표현할 수 있었어요.

왼쪽 matrix는 coefficients matrix라고 이전 포스팅에서 설명을 드렸는데, 2행 3열의 값을 보면 0이 들어간 걸 확인할 수 있죠. 이를 조합의 형태로 나눠본다면 다음과 같이 나눌 수 있어요.

coefficient matrix를 column별로 나눠서 variable matrix의 각 행과 곱했습니다. 즉 coefficient matrix를 vector로 쪼갠 뒤에 variable matrix의 각 component와 곱해준 건데요. variable matrix가 실수로 구성이 되어있다는 것을 알고 있기 때문에 각 vector에 할당된 x의 값이 실수인 것을 알 수 있습니다. 따라서 일종의 Scalar가 되는 셈이죠.
즉, 위의 식(a1x1 + a 2x2 + a 3x3 = b)은 조합의 형태라고 할 수 있습니다.
그런데 이 식이 성립되기 위해선 한 가지 조건이 필요합니다. 그 조건을 알기 위해선 Span의 개념을 알아야 합니다.
2. Span
Span : The set of all linear combinations.

span(생성)은 쉽게 말해 벡터가 가질 수 있는 범위를 말합니다. 위의 식은 1부터 p까지 있는 v라는 vector의 조합이니까 'span {V1,..., Vp}'로 표현할 수 있는 것이죠. 그리고 예시로 들었던 식을 span으로 바꿔보면 'span {a1, a2, a3}'로 표현할 수 있겠죠. 아까 말씀드렸다시피 x는 scalar라는 사실을 명심해주세요.
또한 span은 the subset of R^n spanned by V1, ..., Vp로 표현되기도 합니다.

v1과 v2가 nonzero vector이고 둘 중 하나가 다른 vector의 곱으로 이루어진 vetor가 아니라는 조건이 붙을 때 R^3에서 span {v1, v2}은 다음과 같은 좌표평면 상에서의 어떠한 plane을 구할 수 있는 데요. 이는 vector의 각 component는 방향을 내포하고 있는데 3개 component를 가지고 있기 때문에 이는 3차원으로 표현될 수 있습니다. 또한 여기에 곱해지는 scalar는 0을 포함한 실수가 될 수 있기 때문에 span {v1, v2}는 v1과 v2 그리고 0을 포함합니다.
다시 위의 예시로 돌아가서 'a1x1 + a 2x2 + a 3x3 = b'이 성립되기 위해선 조건이 필요하다고 했죠. 이는 바로 b가 'span {a1, a2, a3}'에 속할 때 성립합니다.
이러한 linear combination은 여러 방식으로 사용될 수 있습니다.
3. Matrix Multiplications as column(row) combinations

먼저 column을 vector로 쪼개는 combination의 예입니다.
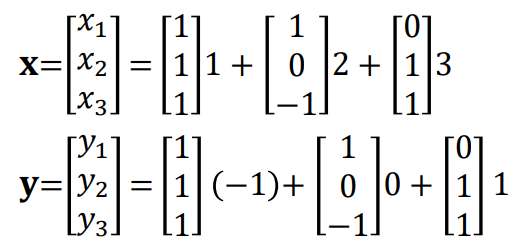
결과 matrix 또한 column별로 쪼개서 각각 combination 간의 곱을 진행할 수 있겠죠.

다음은 row를 vector로 쪼개는 combination의 예입니다.

x와 y vector를 transpose를 시켜 계산하는 것을 확인할 수 있습니다.
사실 처음 vector에 접근하는 입장으로서 직관적으로 이해하기 어려운 내용입니다. 곰곰이 생각해보고 어떻게 이런 방식으로 진행할 수 있는지를 계속 고민하다 보면 이해할 수 있을 것이라고 생각합니다.
간단하게 생각해보면 곱해지는 matrix의 크기에 따라 output되는 matrix의 크기가 달라지는 것을 확인할 수 있었는데요. 이전 포스팅에서 왼쪽에 위치한 matrix의 row의 개수와 오른쪽에 위치한 matrix의 column의 개수가 결과 matrix의 크기를 결정한다고 말씀드렸습니다. 결과 matrix의 크기에 따라 row combination을 진행할지 column combination을 진행할지를 고려해주시면 되는 것 같습니다.
'Mathematics(수학) > Linear algebra(선형대수학)' 카테고리의 다른 글
| 선형대수학 2-2. 부분집합 (0) | 2020.12.22 |
|---|---|
| 선형대수학 2-1. 선형 독립 (0) | 2020.12.22 |
| 선형대수학 1-2. 선형방정식 (0) | 2020.12.20 |
| 선형대수학 1-1. 선형 회귀의 기본 구성요소 (0) | 2020.12.19 |