2020. 12. 22. 21:38ㆍMathematics(수학)/Linear algebra(선형대수학)
이전 포스팅에서 선형 조합에 대해서 알아봤습니다. 이번 포스팅에서는 선형 독립에 대해서 알아보겠습니다.
2020/12/20 - [Mathematics(수학)/Linear algebra(선형대수학)] - 1-2. Linear Equation(선형방정식)
2020/12/21 - [Mathematics(수학)/Linear algebra(선형대수학)] - 1-3. Linear Combinations(선형조합)
참고 : K-Mooc, Mathematical Fundamentals for Data Science. 고려대학교
우선 선형 독립에 대해서 설명하기에 앞서 이전 포스팅의 예시를 다시 들고와볼게요.
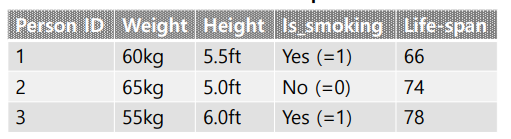

이전 포스팅에서 계속 나온 예시입니다. 이전에 예시를 들었을 때 해가 존재하기 위해선 'b가 span {a1, a2, a3}'에 속해야한다고 설명을 드렸었죠. 그렇다면 어떤 경우에 하나의 해만 가질 수 있는 걸까요? 이를 위해 선형적으로 독립적이다는 개념을 설명해야합니다.
1. 개념
linearly dependent(선형적으로 종속적) : 같은 span에 서로 겹치는 vector가 존재하는 경우
linearly independent(선형적으로 독립적) : 각 vector들의 span이 겹치지 않고 서로 독립적인 경우
정의만 가지고 이해하기에는 상당히 추상적입니다. 예시를 하나 들어볼게요. V1 ~ Vp까지의 vector set이 존재한다고 할 때, Span {V1, ..., Vp-1}에 Vp가 속해있다면 해당 vector set은 선형적으로 종속적이라는 것을 알 수 있겠죠. 왜냐하면 같은 span에 서로 겹치는 vector가 존재하기 때문이죠.
위에서 설명드린 하나의 해만 존재하기위한 조건은 바로 a1, a2, a3가 선형적으로 독립적이어야 한다는 것입니다.
개념을 이해하기 위해서 조금 더 예시를 들고 와볼게요.

다음과 같은 식이 있다고 가정을 해봅시다. 이 경우에는 모든 x set이 0인 경우가 존재합니다. 이러한 해(solution)를 trivial solution이라고 합니다. 이전 포스팅에서 배운 span도 0을 포함한다고 했었죠? 그때 설명드린 '0'이 trivial solution인 경우를 말하는 겁니다.

trivial solution만이 위 식의 유일한 해인 경우엔 V1, ..., Vp가 선형적으로 독립적이라고 할 수 있겠죠. 하지만 그외의 경우가 존재한다면 V1, ..., Vp는 선형적으로 종속적이라고 설명할 수 있어요. coefficient(X)가 0이 아닐 때 위의 식이 성립하는 경우도 선형적으로 종속적인 경우에 해당돼요.
notrivial solution이 있다고 가정하면, 위의 식에서 XjVj를 제외한 나머지를 좌변으로 옮길 수 있어요.

여기서 Xj가 0이 아니면 양변에 Xj를 나눌 수 있겠죠. 그러면 다음과 같은 식이 나옵니다.

그렇게 되면 Vj는 Span {V1, V2, ..., Vj-1}에 속하게 되기 때문에 이는 선형적으로 종속적이게 됩니다.
2. 선형적으로 종속적인 경우의 span
만약 선형적으로 종속적인 vector가 추가가된다면 어떻게될까요?

다음과 같이 Span {V1, V2}에 V1, V2에 선형적으로 종속적인 관계인 V3가 추가된다고 가정합시다. 그렇다면 해당 span은 어떻게 될까요? 답은 변화가 없다입니다. 왜 그렇게 될까요?
'V3 = d1V1 + d2V2'라고 가정해봅시다. 그렇다면 선형조합 하에서 v1, v2, v3는 다음과 같이 쓸 수 있겠죠.

그렇다면 이건 V1, V2의 선형 조합으로 바꿀 수 있고 결국 V3를 추가한다고 해도 이는 span {V1, V2}에 포함된다고 할 수 있습니다. 즉, span {V1, V2, V3}와 span {V1, V2}가 같다는 의미인거죠.

재미있는 점은 vector의 크기와 차원으로도 선형적으로 종속적인 관계를 확인할 수 있는 게 있습니다. R^3에 속하는 vector 5개가 존재한다고 가정해봅시다. 쉽게 생각해 3 x 5 matrix가 있다고 생각하시면 됩니다. 이를 5 x 1 vector와 곱하게 되면 3 x 1 vector로 결과값이 나옵니다.
vector가 모두 R^3에 속하기 때문에 이는 3차원 상에서 표현이 가능합니다. 이때 이전 포스팅에서 설명드렸다시피 V1, V2, V3가 선형적으로 독립적이라면 span {V1, V2, V3}는 3차원 공간을 모두 다 포함하는 것을 알 수 있습니다. 만약 여기에 V4, V5가 추가된다면 이는 3차원 공간내에서 span {V1, V2, V3}와 겹치지 않고 표현할 수 없기때문에 이는 선형적으로 종속적일 수 밖에 없습니다.
이전에 설명드린 variable의 개수가 equation의 개수보다 많은 경우인 'under-determined system'의 상황이 됩니다. 즉 해가 무수히 많아질 수 있는 것이죠.
상당히 추상적인 내용이다보니 점점 어려워지고 있는 것 같습니다. 꾸준히 이전 내용들을 복습하면서 공부를 해야지 계속 진도를 나갈 수 있을 것 같습니다. 하지만 이전에 추상적으로 배웠던 내용들이 배워가고 있는 내용과 겹치면서 머릿속에서 선형대수학이라는 얼개가 점점 촘촘해지는 것 같습니다.
'Mathematics(수학) > Linear algebra(선형대수학)' 카테고리의 다른 글
| 선형대수학 2-2. 부분집합 (0) | 2020.12.22 |
|---|---|
| 선형대수학 1-3. 선형조합 (0) | 2020.12.21 |
| 선형대수학 1-2. 선형방정식 (0) | 2020.12.20 |
| 선형대수학 1-1. 선형 회귀의 기본 구성요소 (0) | 2020.12.19 |