2022. 3. 7. 16:18ㆍ강의 내용 정리/확률및랜덤변수
확률공리와 확률 이론
1. 확률 공리(Probability Axiom)
- 확률에 대한 가장 기초적이며 증명할 필요가 없는 명제로, 확률에 대한 여러 정리를 이끌어내는 기초가 된다.
1) 공리1: 모든 사건에 대해 그 사건의 확률은 0보다 크거나 같다. (음수가 없다.)
2) 공리2: Sample Space를 사건으로 갖는 확률은 1로 한다.
-> 실험으로부터 나올 수 있는 모든 실험 결과를 가지고 있는 집합을 사건으로 갖는 확률은 1로 한다. -> 반드시 발생할 사건에 대한 확률은 1로 한다.
3) 공리3: mutually exclusive한 사건(서로 동시에 발생할 수 없는 사건)들에 대한 합집합과 각각의 사건에 대한 확률을 더한 한 확률은 동일하다.
cf) 만약 A, B, C가 mutually exclusive하다면 P(A U B U C) = P(A) U P(B) U P(C)이다.
즉, 첫번째 공리와 두번째 공리는 확률이 0과 1 사이의 값이 되어야한다는 것을 의미하고, 세번째 공리는 상호배타적인 사건이 발생할 확률은 각각의 사건이 발생할 확률의 합임을 의미한다.
<확률 공리를 이용한 동전 던지기의 확률 구하기 예제>
S = {H, T}
공리 1: P{H} >= 0, P{T} >= 0
공리 2: P{S} = P({H, T}) = 1
공리 3: P({H, T}) = P({H}U{T}) = P({H}) + P({T}) = 1
모델: P({H}) = P({T})
P({H}) = P({T}) = 1 / 2
2. 기본적인 확률 이론
1) 확률 이론 1.1: 상호배타적인 사건 2개의 합은 각각의 사건이 발생할 확률의 합과 동일하다.
2) 확률 이론 1.2: 상호배타적인 사건 여러 개의 합은 각각의 사건이 발생할 확률의 합과 동일하다.
3) 확률 이론 1.3
(1) 공집합의 확률은 0이다.
S = S U 공집합
P{S} = P{S} + P{공집합} <- 공리 3(상호 배타적)
P{공집합} = 0
(2) 어떤 여집합의 확률은 '1 - 그 사건이 발생할 확률'이다.
S = A U A^c <- 공리 3(상호배타적)
P{S} = P{AUA^C} = P{A} + P{A^c}
(3) 모든 A와 B 사건의 확률 합은 '각 사건의 확률 합 - 두 사건의 교집합이 되는 사건의 확률'이다.
-> 30 페이지 증명과 비슷
(4) 만약 사건 A가 사건 B의 부분집합이면 사건 A의 실험 결과는 사건 B의 실험 결과에 포함되기에 A가 발생할 확률은 B가 발생할 확률보다 작거나 같다.
4) 확률 이론 1.4: 사건 B가 발생할 확률은 사건 B의 실험 결과들이 각각 발생할 확률의 합과 같다.
ex) 주사위를 던지는 실험
S = {1, 2, 3, 4, 5, 6}
A = {짝수} = {2, 4, 6}
P{A} = P[{2}] + P[{4}] + P[{6}]
A = {s1, s2, s3} = {s1} U {s2} U {s3} <- 상호배타적
P{A} = P[{s1} U {s2} U {s3}] = P[{s1}] + P[{s2}] + P[{s3}] <- 공리 3
5) 확률 이론 1.5: 동일한 전체 집합에서의 실험결과가 동일하게 발생한다면 1 <= i <= n에 대해 P[{Si}] = 1 / n 이다.
S = {s1, s2 ... sn}
P[{s1}] = P[{s2}] = ... = P[{s3}]
P[S] = 1
P[{s1 ... sn}] = P[{s1} U ... U {su}] = P[{s1}] + ... + P[{sn}]
cf 1) all faces are equally likely와 같이 모든 사건이 발생할 확률이 동일하다는 내용이 있어야지 해당 이론 사용 가능
cf 2) 사건은 집합이기 때문에 P[{s1}]로 사용하는게 맞음
예제) 주사위 던지기 실험에서 모든 주사위의 눈이 나올 확률이 동일하다고 할 때 4 이상의 눈이 나올 확률과 짝수가 나올 확률을 구하시오.
A = {4이상} = {4, 5, 6}
B = {even} = {2, 4, 6}
P{A} = P[{4}] + P[{5}] + P[{6}] = (1.4 이론에 의해) 1/6+1/6+1/6 = 1/2
P{B} = P[{2}] + P[{4}] + P[{6}] = (1.4 이론에 의해) 1/2
3. 조건부 확률
- 어떤 사건이 발생할 확률은 어떤 실험결과가 나온다는 것은 알지 못한다.
ex) 짝수눈이 발생한 확률 -> 2가 나올지, 4가 나올지, 6이 나올지 모르기 때문.
- 하지만 어떤 실험 결과의 부분적인 정보가 주어졌을 때 어떤 실험결과가 나올 확률이 달라진다.
ex) 주사위를 두번 던졌을 때 첫번째 주사위의 눈이 6이 나올 확률은 그냥 주사위를 굴렸을 때 주사위의 눈이 6이 나올 확률과 다르다.
- 조건부 확률은 사건 A와 사건 B의 교집합이 존재하지 않는 경우에는 조건부확률이 0이기에 사건 A가 발생할 확률보다 조건부 확률이 꼭 높다고만 할 수는 없다.
1) 조건부 확률 공식
사건 B가 발생했을 때 사건 A가 발생할 확률: P{A|B} = P{{A와 B의 교집합}} / P{B}
예제) 52개의 카드를 섞은 뒤 하나를 뽑을 때 바닥에 있는 카드가 검은색 카드라고 했을 때 그 카드가 스페이스(clubs) 에이스일 확률은? 이때 모든 카드가 뽑힐 확률은 equally likely함
A: ace of club
B: black card
P[{A|B}] = P[{A와 B의 교집합}] / P[{B}] = (1/52) / (1/2) = 1/26
P[{B}] = 26/52 = 1/2
P[{A와 B의 교집합}] = 1 / 52
예제)
A: 비행기가 출현한 사건
D: 비행기가 감지되고 경보가 울리는 사건
P[{D|A}] = 0.99
P[{D|A^c}] = 0.1
P[{A}] = 0.05
i) 비행기가 없는데 경보가 울릴 확률
P[A 교집합 A^c] = P[D|A^c] x P[A^c] = 0.1 x (1-0.05)
ii. 비행기가 있는데 경보가 울리지 않는 사건
4. 파티션
- A, B, C가 파티션이다 -> A, B, C는 동시에 발생하지는 않지만 셋 중 하나는 반드시 발생해야한다.
예제) 동전 4번 던지기
- 앞면이 0개, 1개, 2개 나올 사건의 집합은 파티션이 아니다 -> 전체망라적이지 않기 때문이다.
1) 확률 이론 1.7: 파티션인 집합 B{B1, B2, B3 ...}에 대해 사건 A가 있을 때 A와 Bi의 교집합의 합집합은 A가 된다.
ex) 경영대 = {경영학과, 회세}, F = {여학생}, F = (경영학과와 여학생의 교집합) U (회세와 여학생의 교집합)
2) 확률 이론 1.8: 1.7 이론을 확률로 풀이한 것
3-1) Law of total probability(전체 확률의 법칙)
- 문제를 잘게 쪼개서(분할정복, divide-and-conquer) 문제에 접근하는 것
3-2) 확률 이론 1.9: 1.8 이론을 조건부 확률로 표현한 것
예제) 주머니 안에 동전 3개(H/T, H/H, T/T)를 던져서 앞면(H)이 나올 확률은?
H: 앞면, 파티션 {C1, C2, C3}
-> P[H] = P[H|C1]P[C1] + P[H|C2]P[C2] + P[H|C3]P[C3] = 1/2 x 1/3 + 1 x 1/3 + 0 x 1/3 = 1/2
P[{실험결과를 원조로 하는 집합}] -> 집합인 경우에는 {}로 표현함
4) 확률 이론 1.10(베이즈 정리)

- 이때 아래 정리는 Bk가 파티션이어야하고 사건 A는 관찰할 수 있지만 파티션 B는 관측할 수 없음
예제)
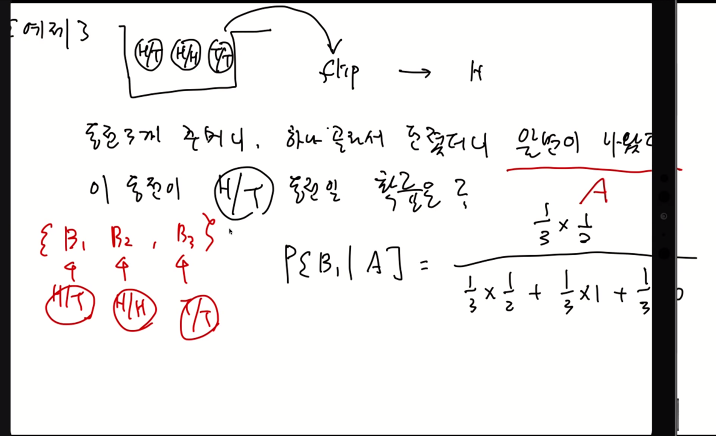
- 베이즈 정리란 어떤 사건이 발생했을 때 어떤 것을 통해서 발생했는지 확률을 구하는 것을 의미함
- 베이즈 정리란 논리적인 인과성을 판단하기도함
ex) 사건 A가 발생했을 때 파티션 B2가 사건 A를 일으킬 가능성은?
5. 독립
- 사건 A, B가 독립인 경우 사건 A의 발생이 사건 B의 발생확률에 영향을 미치지 못한다.
- P[A와 B의 교집합] = P[A]P[B]인 경우엔 두 사건이 독립이다.
- P[A와 B의 교집합] = P[A]P[B]와 동치: P[B] = P[B|A], P[A] = P[A|B]
- 세 개의 사건의 경우 다음 네가지 조건을 만족시켜야함

예제)
s = {B1, B2, W3, W4}, B는 검은색 공, W는 흰색 공
A는 검은색 공을 꺼낼 확률
B는 짝수 공을 꺼낼 확률

cf) mutally exclusive는 독립과는 다르다. 왜냐하면 상호 배타적인 경우에는 하나가 발생하면 다른 게 발생하지 않기 때문
세 가지 사건에 대한 독립 예제)
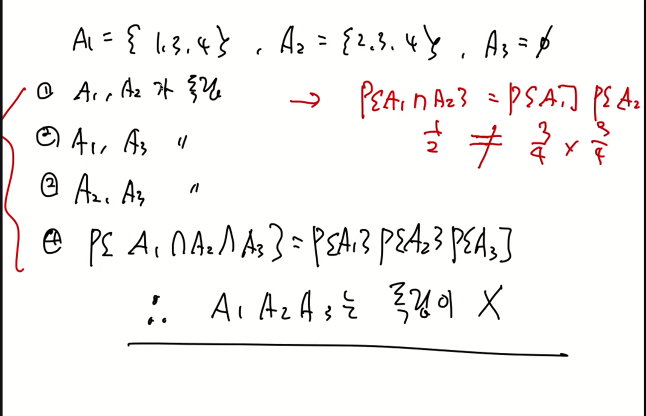
- n개의 사건이 독립일 조건은 다음과 같음

'강의 내용 정리 > 확률및랜덤변수' 카테고리의 다른 글
| 확률 및 랜덤변수(6), 연속랜덤변수 (1) | 2022.05.09 |
|---|---|
| 확률 및 랜덤변수(5), 통계와 확률 (0) | 2022.04.16 |
| 확률 및 랜덤변수 (4), 이산랜덤변수 (0) | 2022.04.15 |
| 확률 및 랜덤변수 (3), 순차 확률 (0) | 2022.03.22 |
| 확률 및 랜덤 변수, 확률(1) (1) | 2022.03.07 |