2022. 5. 9. 20:33ㆍ강의 내용 정리/확률및랜덤변수
연속랜덤변수
- 치역이 셀 수 없는 집합인 경우 ex) 랜덤변수의 값이 실수값을 가지는 경우
- 연속적인 실수 변수 값을 가지는 경우에는 연속 랜덤변수라고 함
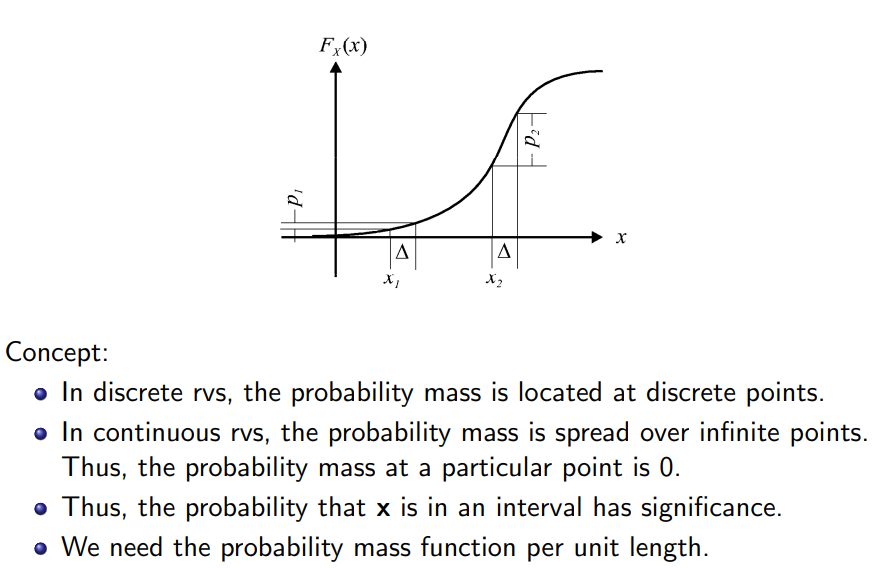
- 연속랜덤변수의 특징: 연속랜덤변수 x가 특정 실수 값을 가질 확률은 0이다. 하지만 특정 구간에 대해서는 확률 질량 값이 존재한다.
연속랜덤변수 각각에 대응되는 확률을 다 합치면 1인데 연속랜덤변수는 셀 수 없기에 특정 실수값에 대응되는 확률이 0이되고 PMF의 값은 0이 된다.

예시

- 연속랜덤변수의 경우에는 부피, 공간 등에 대해 확률 밀도라는 지표로 확률 모델을 설정함


밀도와 부피를 곱한 것의 적분한 것이 질량이기에 이를 통해 확률을 알 수 있다.
CDF
- PMF는 이산랜덤변수에서만 사용가능하지만 CDF는 이산/연속랜덤변수 모두에서 사용가능하다.
CDF의 정의

CDF의 특징

이산랜덤변수와 연속랜덤변수에서의 CDF 차이점은 이산랜덤변수는 불연속 함수였지만 연속랜덤변수는 연속함수라는 점이다. 이는 랜덤변수 x의 치역이 아닌 곳에서 불연속이 생긴다.

- CDF가 연속이면 연속랜덤변수이다.
- 이를 활용해 연속랜덤변수와 이산랜덤변수를 구분할 수 있다.
예제)

풀이)

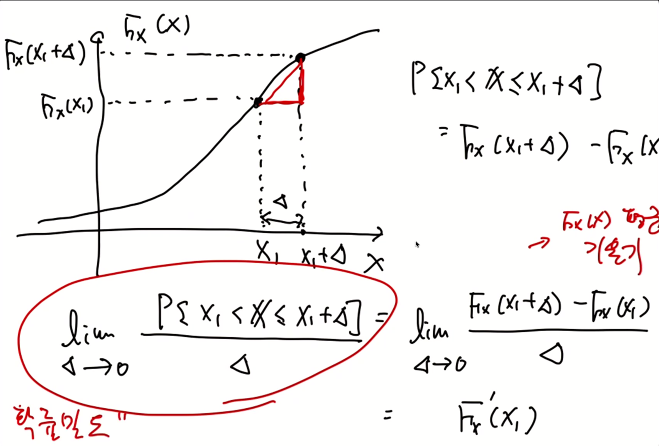
좌측식이 확률 밀도가 된다.
pdf 정의
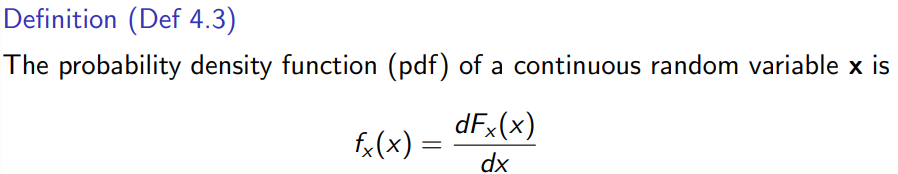
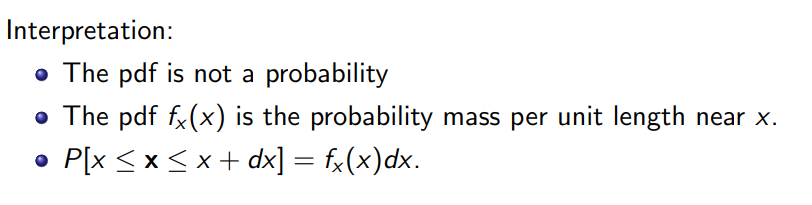
pdf는 확률 자체를 의미하는 것이 아닌 밀도를 의미한다.
예제)
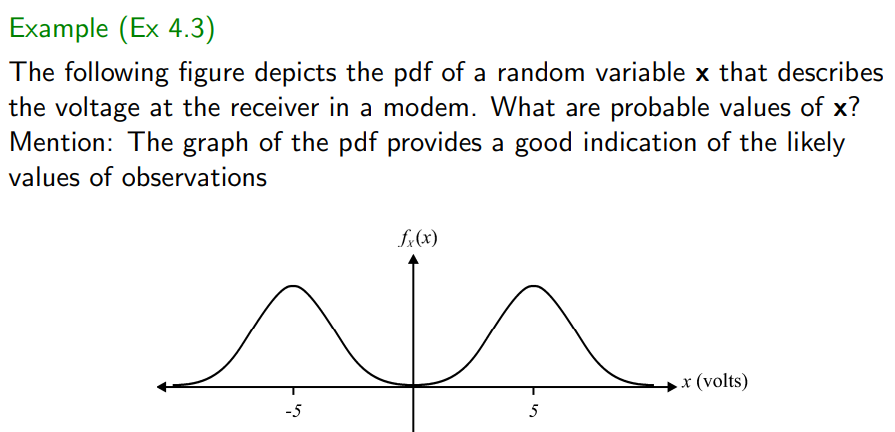
+-5부근에 있는 값이 확률 밀도의 값이 가장 크다.

- CDF는 비감소함수이기에 이의 미분값인 PDF는 항상 0 이상이다.
- PDF를 적분하면 CDF가 된다.
- PDF의 모든 범위에 대한 적분은 1이다.
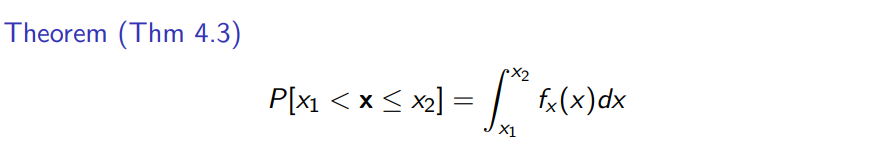
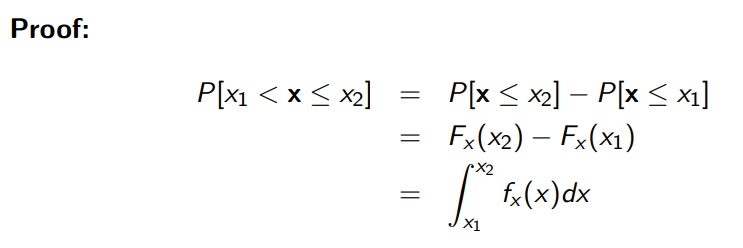
그림
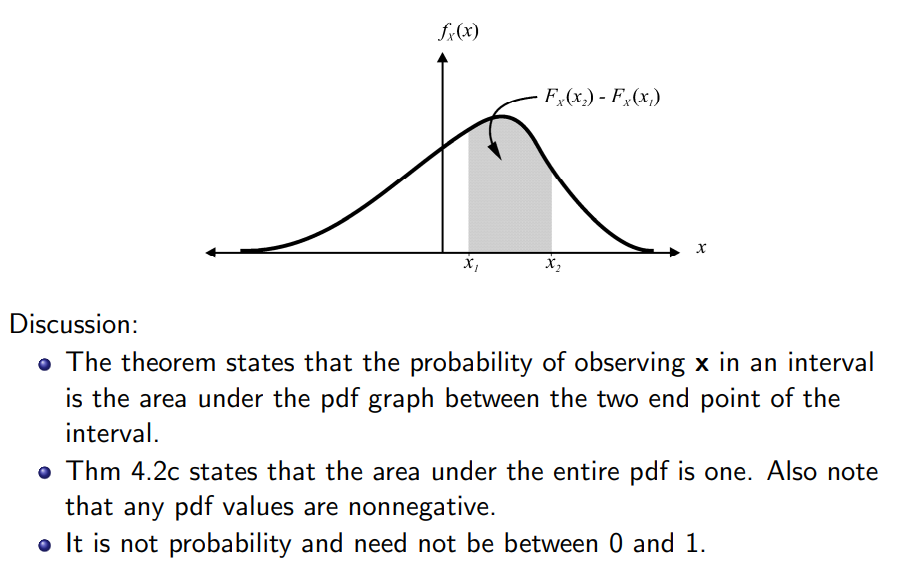
예제)

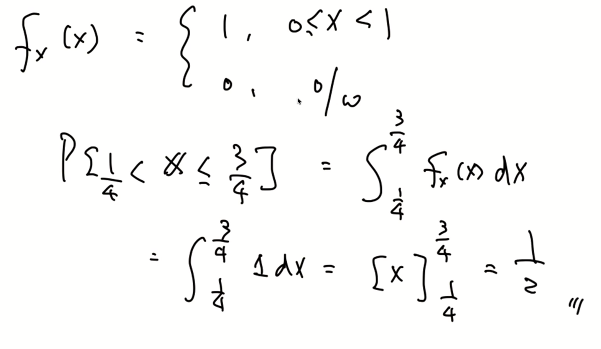
예제)

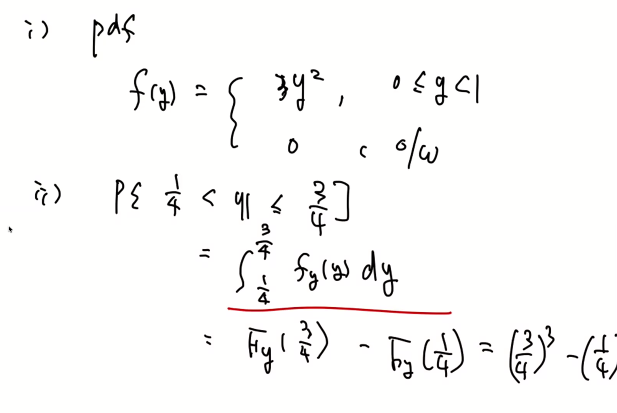
이산 랜덤변수에서의 값 포함 유무
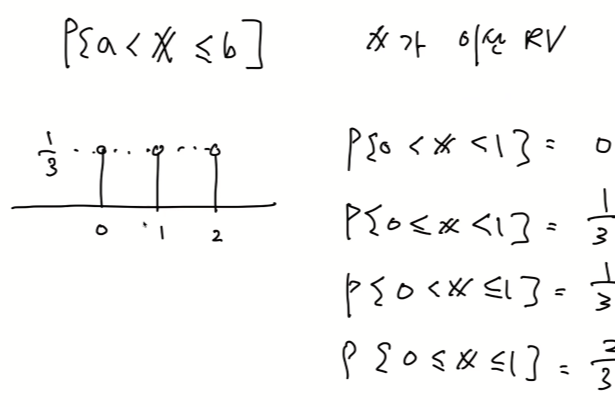
연속 랜덤변수에서의 값 포함 유무
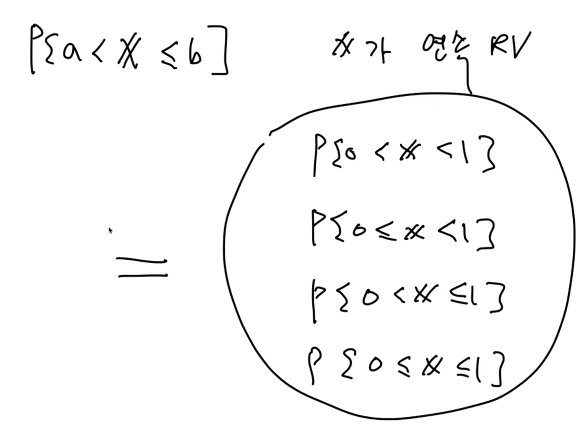
기대치
기대치를 구하기 위해서 연속 랜덤변수를 이산 랜덤변수화시킨다.

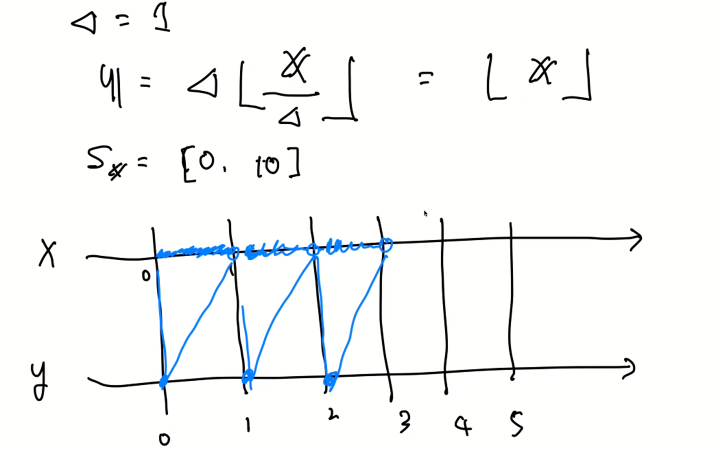
y의 치역은 증분을 통해 표현할 수 있다. 이에 따라 기대치를 구할 수 있다.
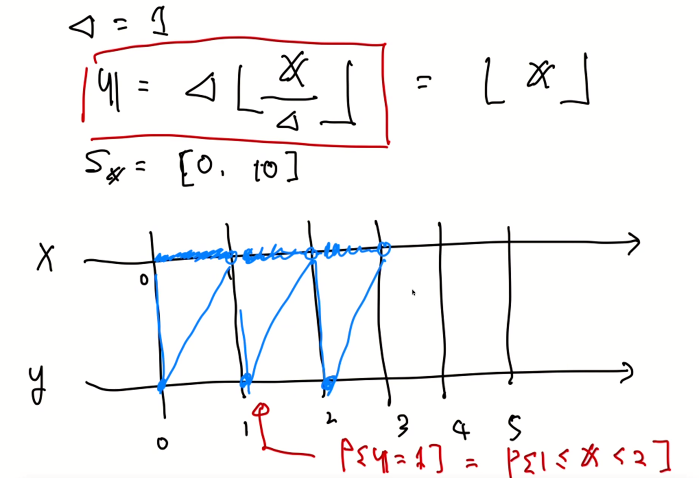
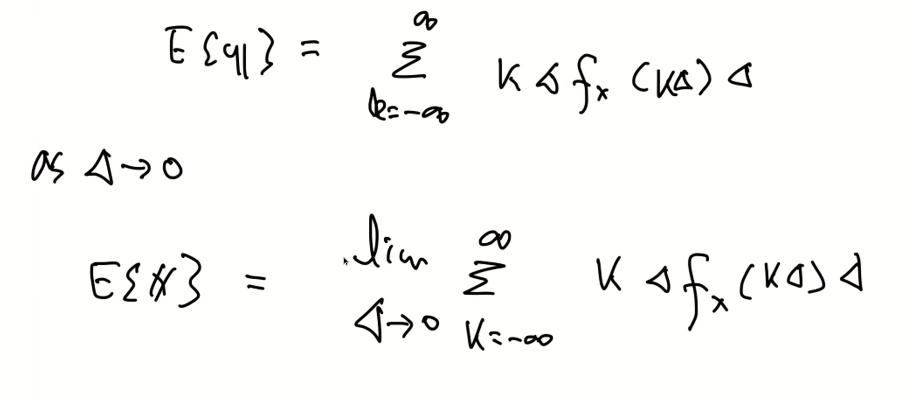
기대치 정의
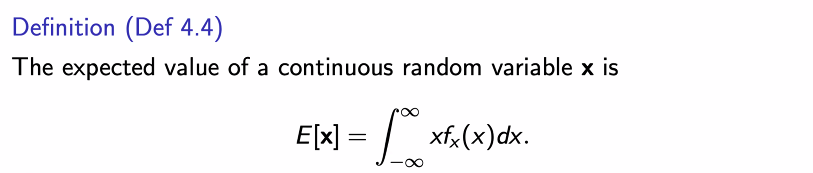
예제)

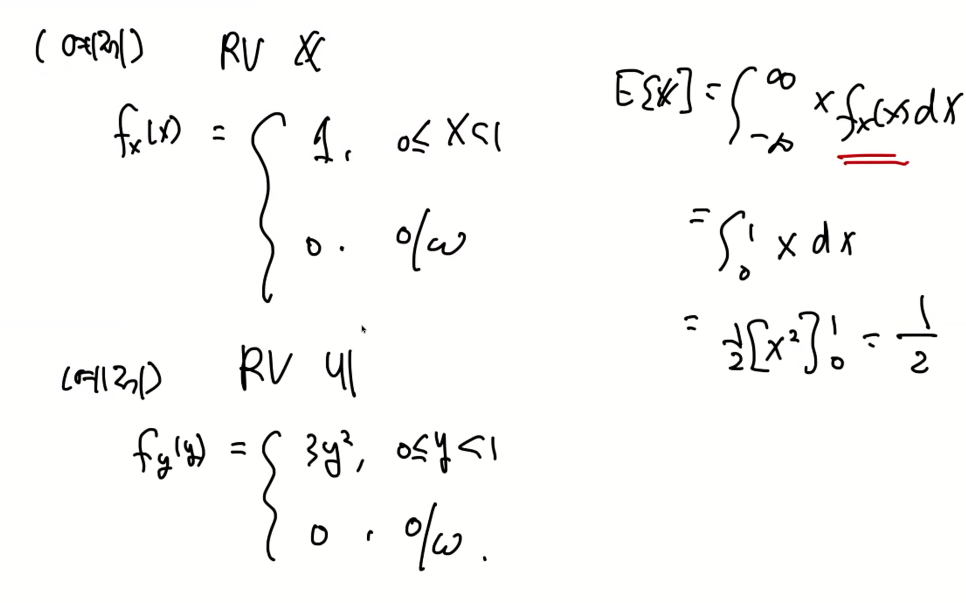
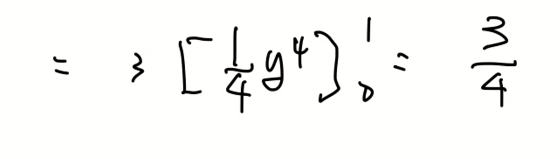
랜덤변수 x에 대한 함수 y는 연속/이산 모두 가능하다.
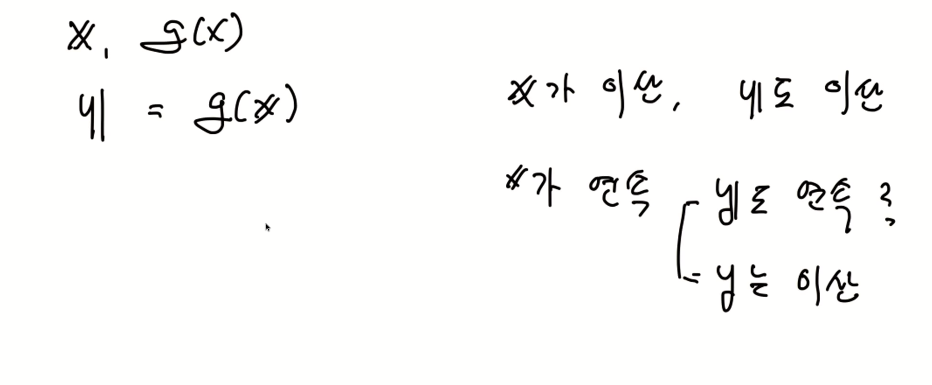
예제)
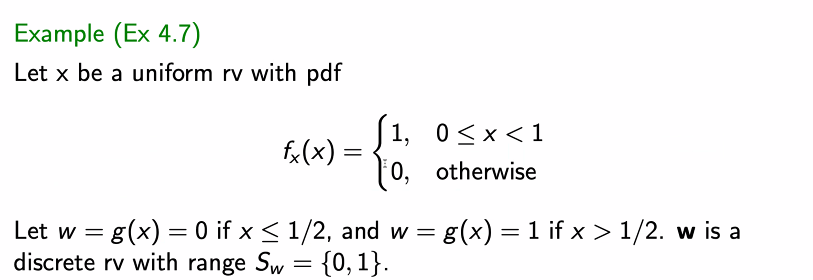
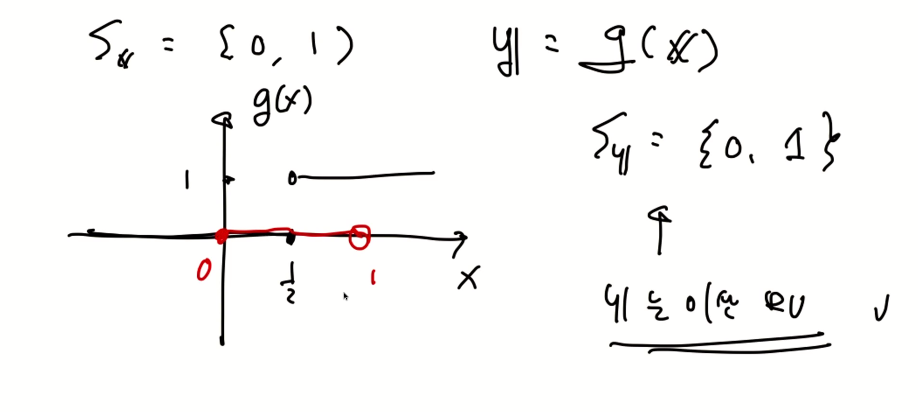
연속 랜덤변수도 이산랜덤변수와도 비슷한 성질이 등장한다.

Uniform 연속 확률 분포

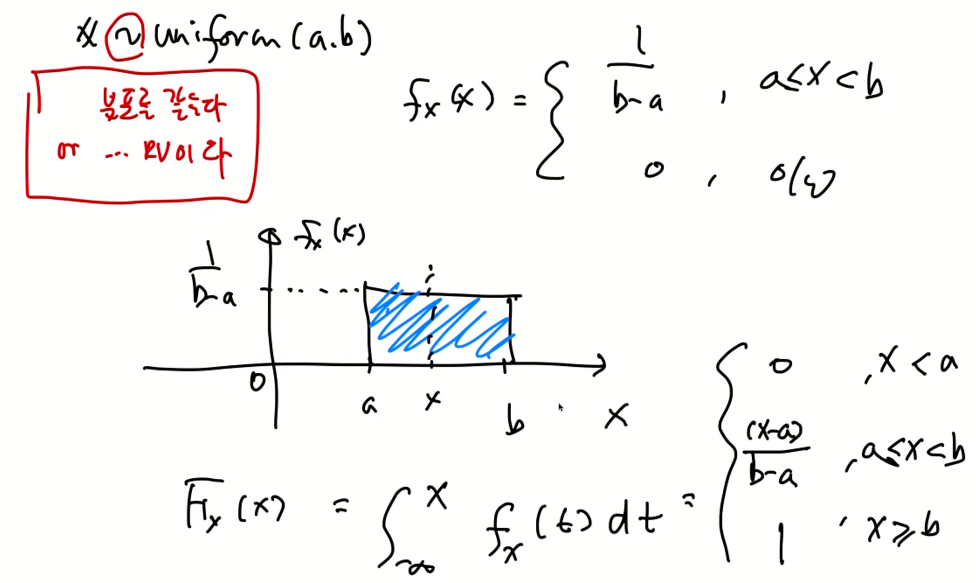
예제)

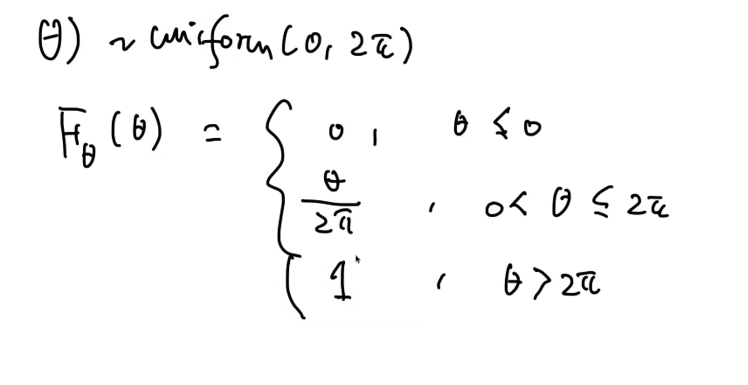
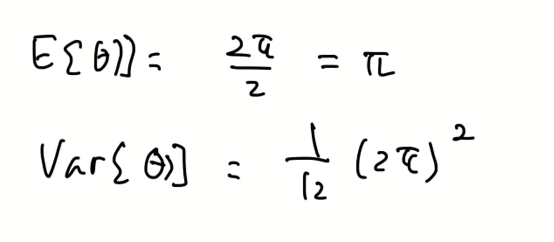

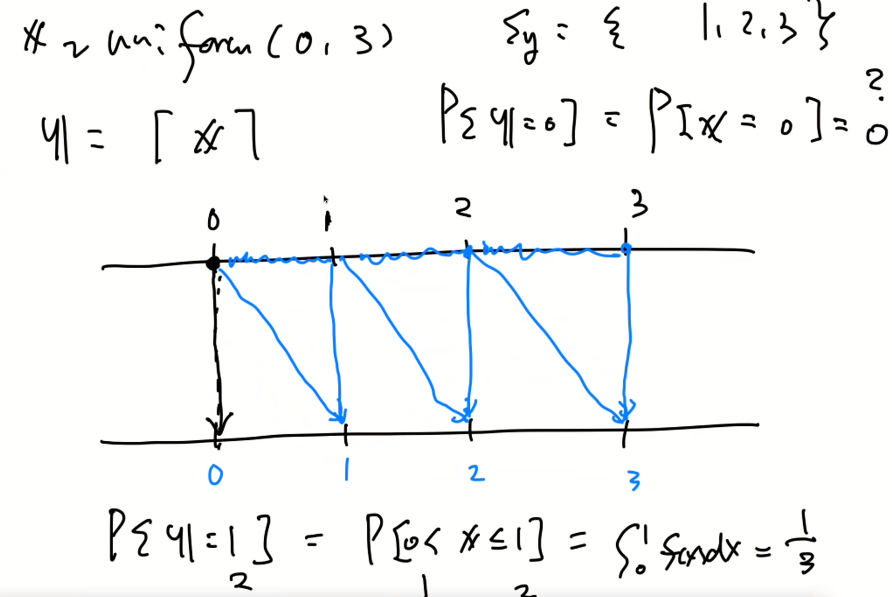
랜덤변수 y가 0이되기 위해서는 x는 0의 값을 가져야한다. 이때의 확률값은 0이다. y가 1일 때는 1/3 확률이다.
이를 정리하면 다음과 같다.
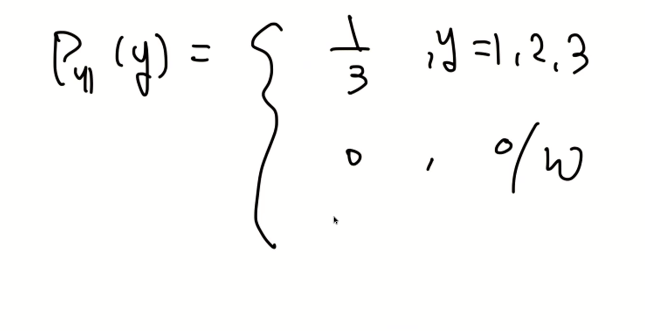
exponential

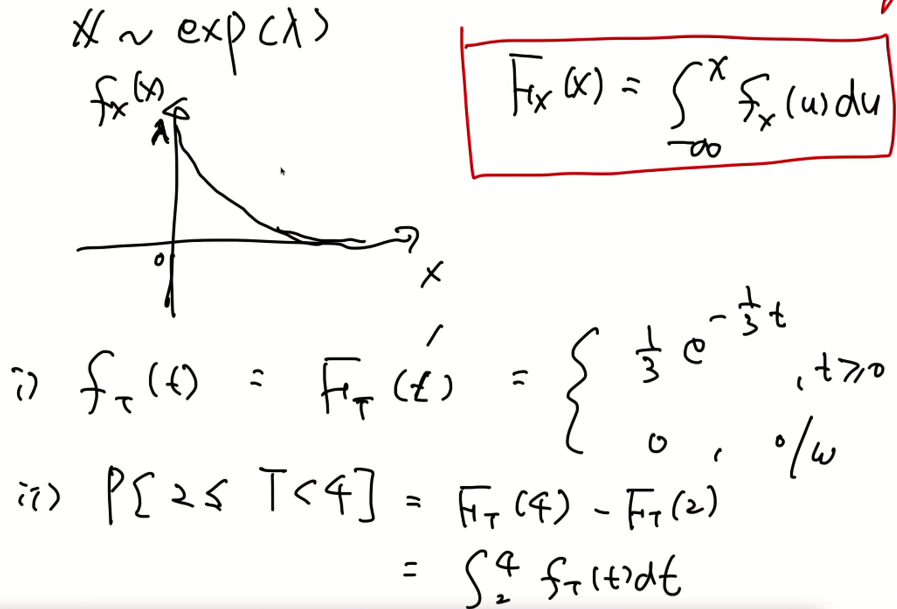
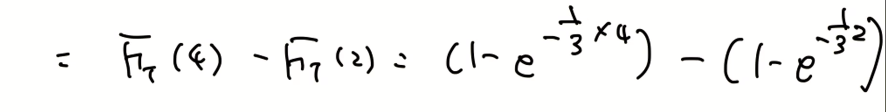
pdf보단 cdf가 더 쉽다.
예제)

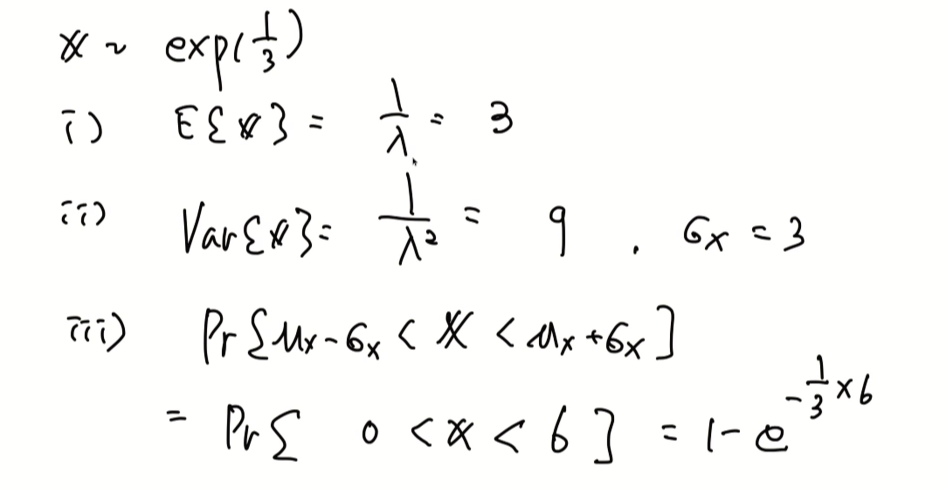
연속 exponential 랜덤.변수의 친척은 이산 geometric 랜덤변수이다.
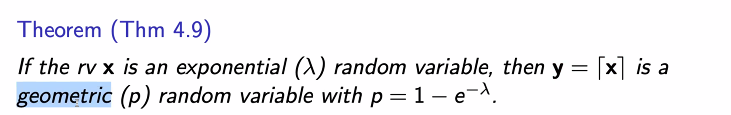
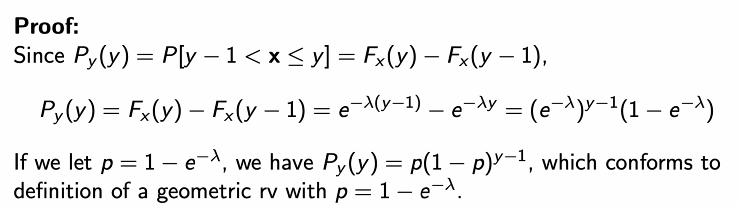
Erlang 랜덤변수
- exponential + exponential
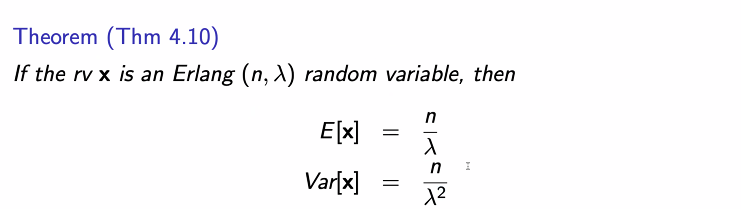
Gaussian 랜덤변수
- normal 랜덤변수라고 하기도 한다. 단 이때 파라미터가 시그마 제곱으로 바뀐다.
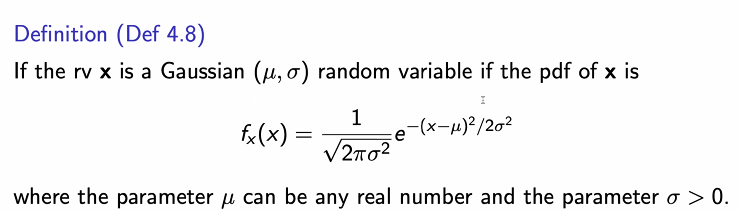
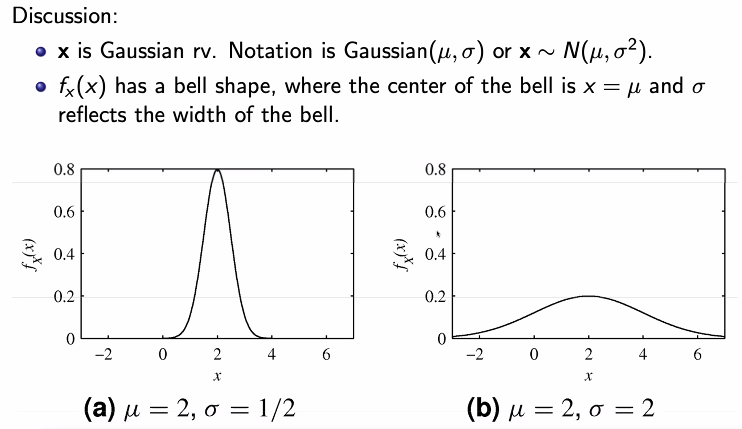
- 종 모양의 우함수이다.
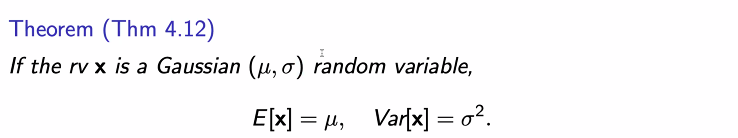
- u를 중심으로 대칭이기에 이 값이 평균이 되고, 시그마는 얼마나 퍼져있나의 정도를 의미하는 것이기에 위의 값이 나온다.
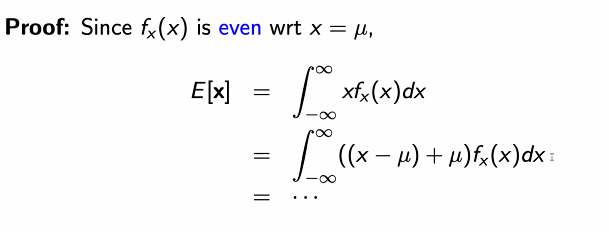
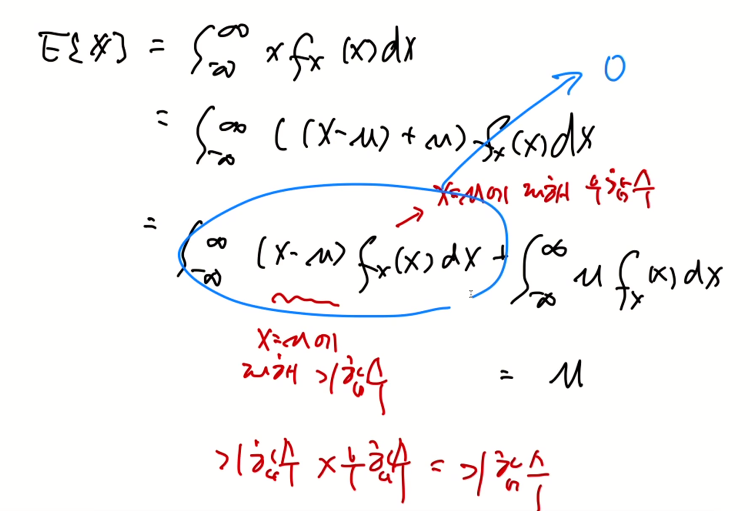
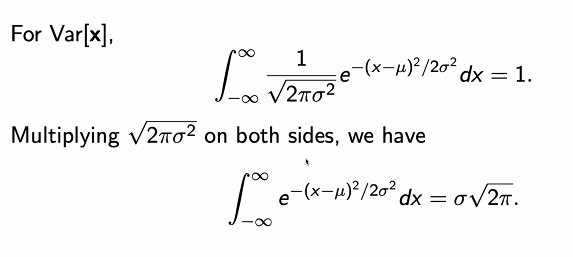
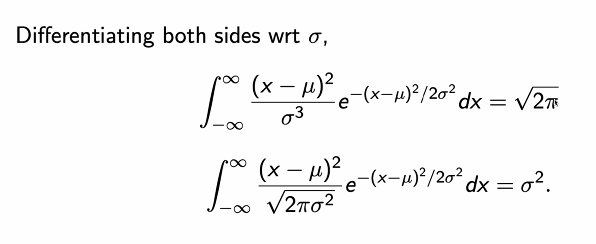
가우시안 함수는 다음과 같이 딱 떨어지는 식으로 계산할 수 없다.
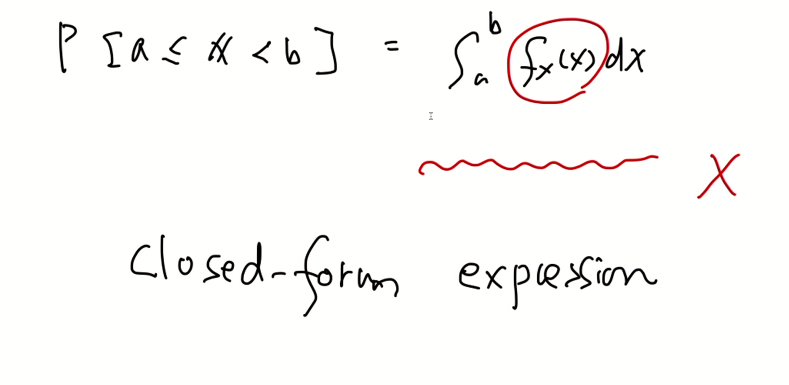

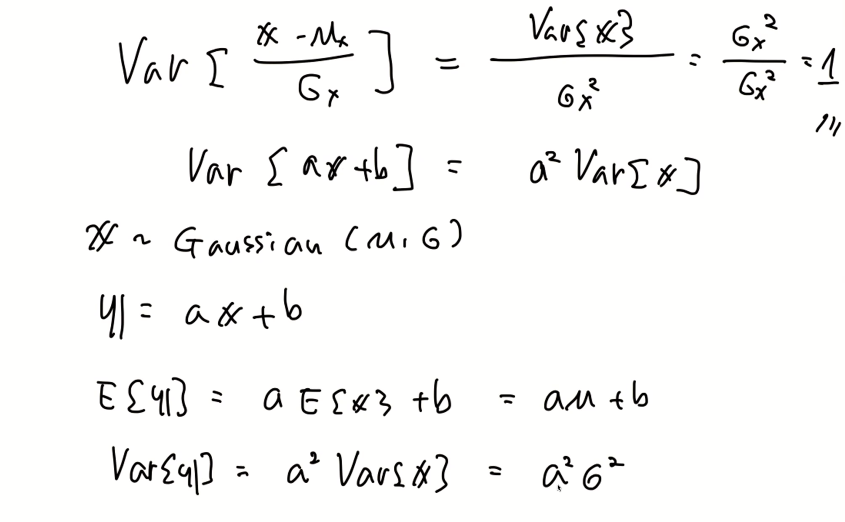
- 이는 기대치와 분산을 알수는 있지만 선형변환의 모습과 분포는 알 수 없다. 따라서 아래의 증명을 거쳐서 구할 수 있다.
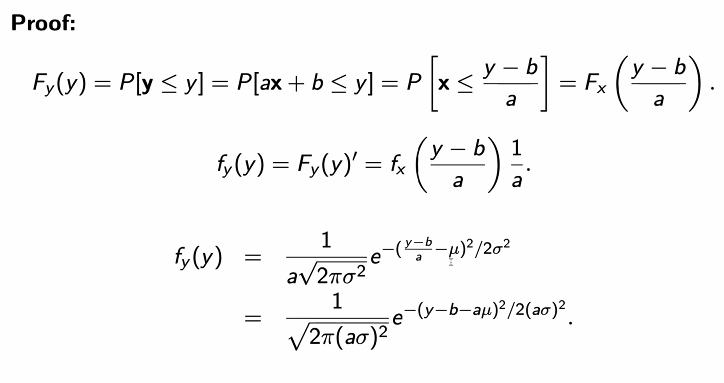
- 가우시안을 선형변환시킨 가우시안 함수의 분포를 확인할 수 있다.
- 가우시안 함수의 선형변환은 가우시안 함수가 되고 해당 분포는 위의 증명을 토대로 알 수 있다.
표준 정규 분포

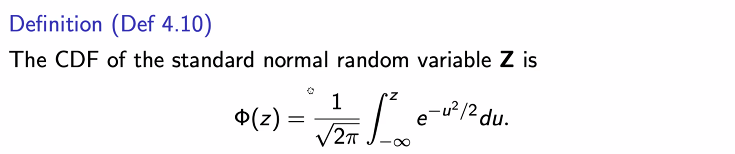
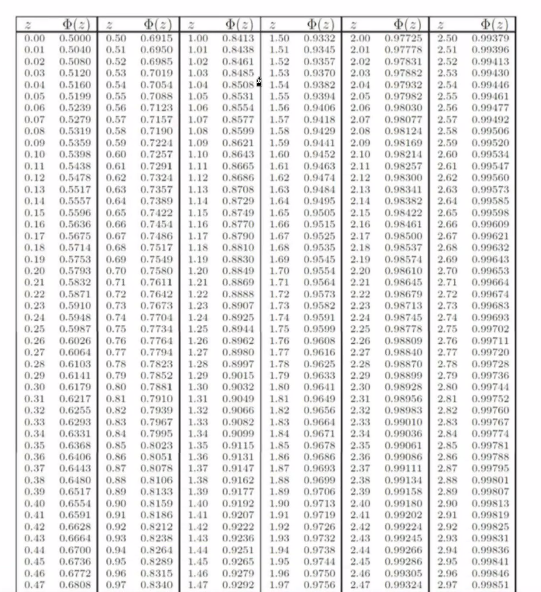


예제)

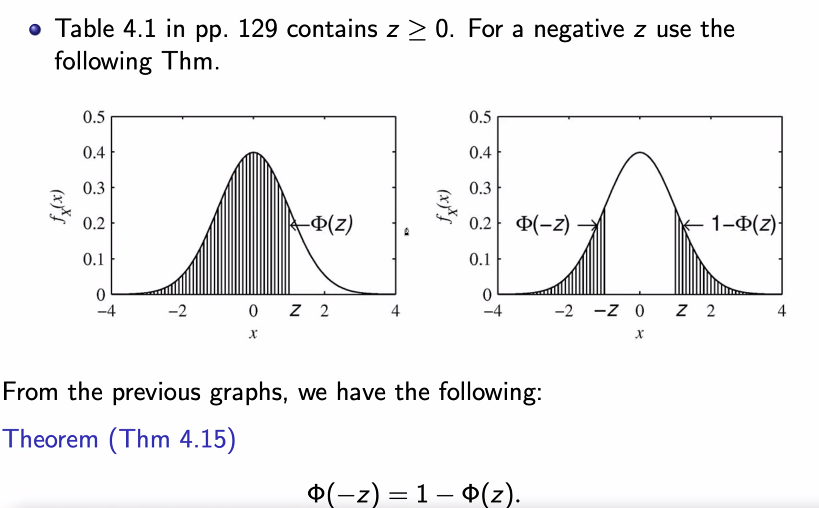
- 대칭이기에 음수는 1 - 양수로 바꿔서 표현한다.
예제)

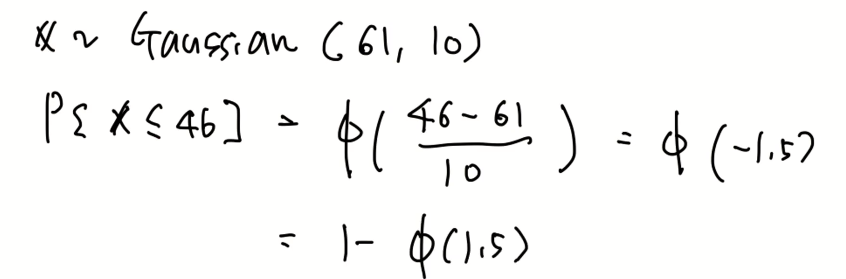
예제)
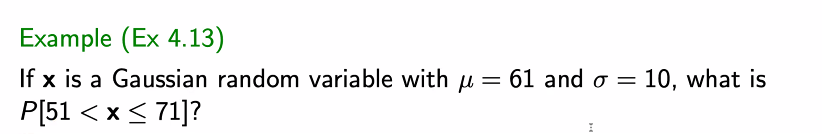
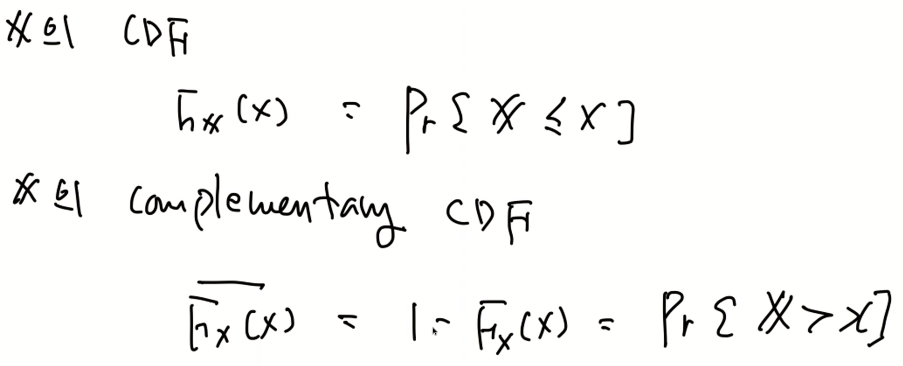

Derived random variable 문제가 나온다.
-> 교재에서는 6장으로 존재
예제)

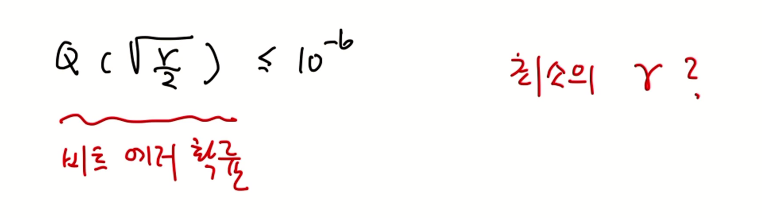
교재에는 Q(4.17)이 10의 -6승보다 작다고 나온다. 이에 따라 다음과 같이 식을 작성할 수 있다.
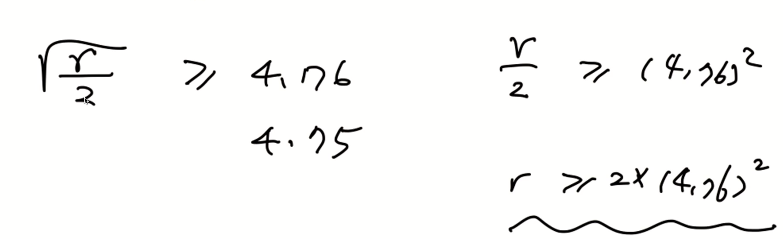
Q(z)의 의미)


- 3번째 랜덤변수에 관한 함수가 존재한다.
- 혼합 랜덤 변수(Mixed random variable): 어떤 구간에 대해서는 연속이며 어떤 구간에서는 이산이기에 연속과 이산의 성격을 모두 가지고 있는 것!
- Mixed Random Variable은 델타 함수를 가지고 표현한다.
델타 함수의 정의
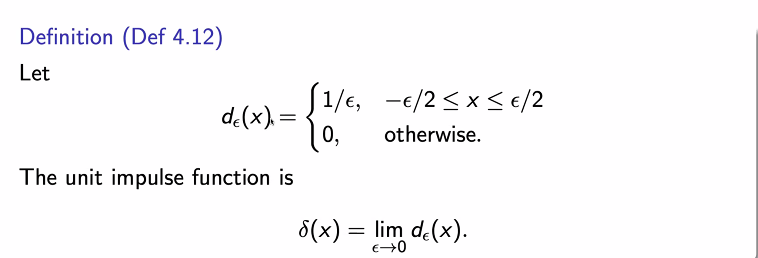
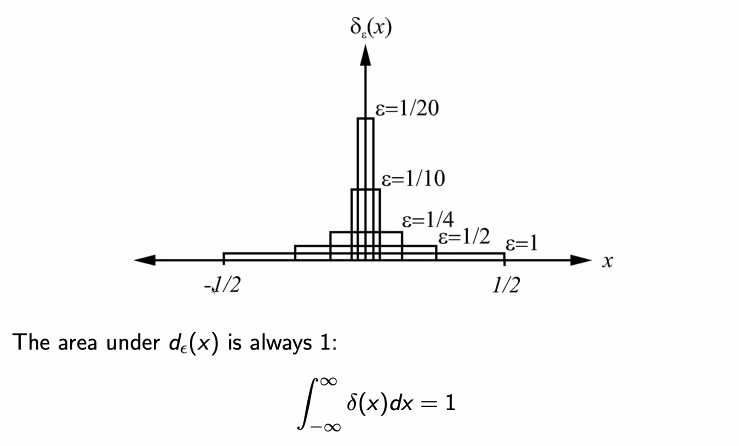
- 입실론이 1/2인 경우에는 -1/4에서 1/4 구간 사이에서 2의 값을 가진다.
- 입실론을 적분하는 경우에는 언제나 1의 값이 나온다.
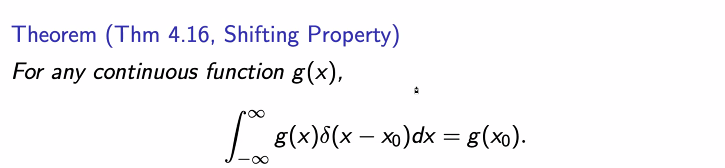
- 깊게 나가지는 x
Unit step Function
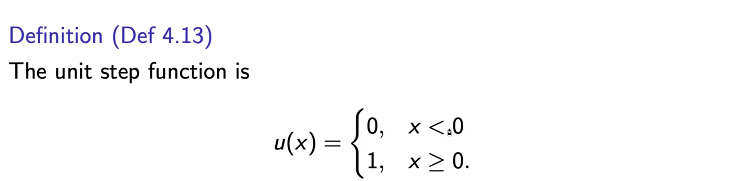
- 델타 함수와는 서로 미분/적분의 관계가 있다.

- 이산랜덤변수에서 각각의 치역에 해당하는 x값과 그에 해당하는 unit step function을 곱한 것을 더한 것과 CDF와 동일하다.
- 현실적으로 이를 사용했을 때 유용성이 있다.
- 아래의 식에서 이를 확인해볼 수 있다.
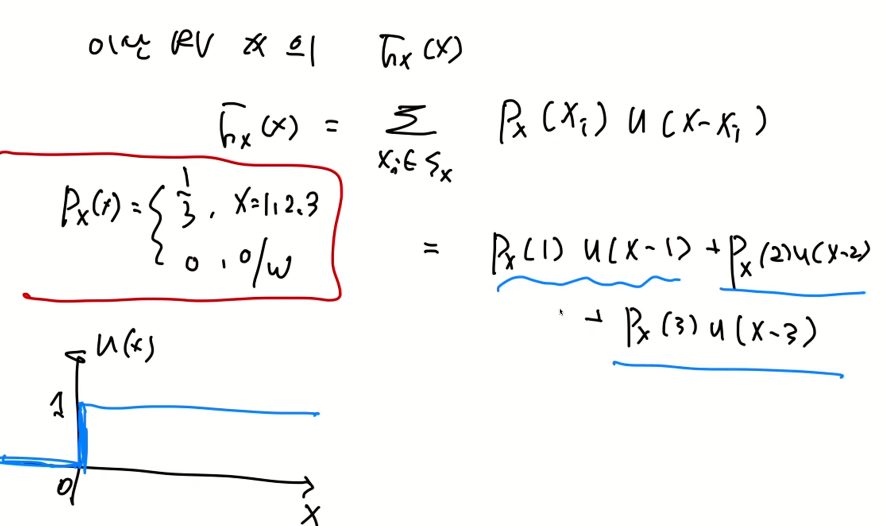
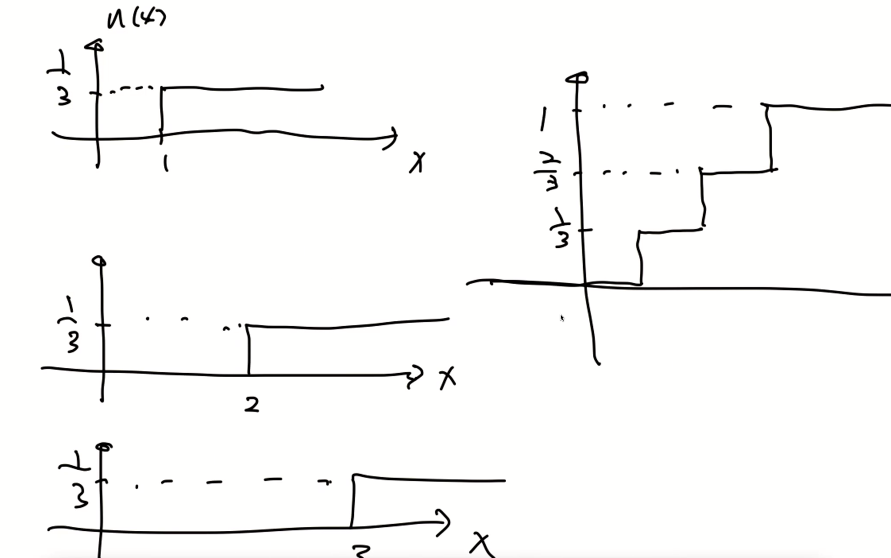

- x1일 때의 값이 P(x1)이 아닌 델타 함수의 계수를 설명하는 것이다.

- Unit step 함수를 통해 CDF를 다음과 같이 표현할 수 있다.
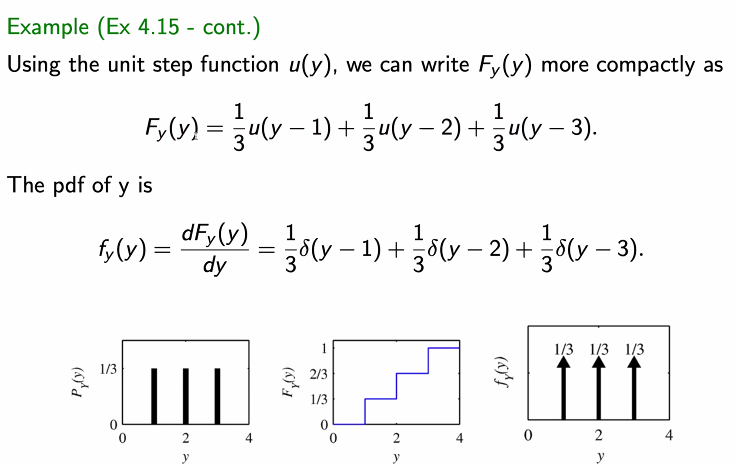
- CDF를 구한 뒤 이를 미분해서 PDF를 구한다. 하지만 사실 혼합 랜덤변수가 아닌 이산 랜덤변수에서는 위와 같이 사용하면 안된다.
- 위와 같이 계수를 사용하는 것은 이후에 유용하게 사용하고자 하는 것이다.
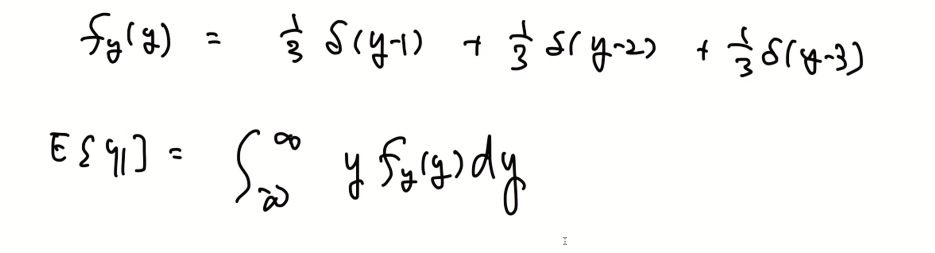
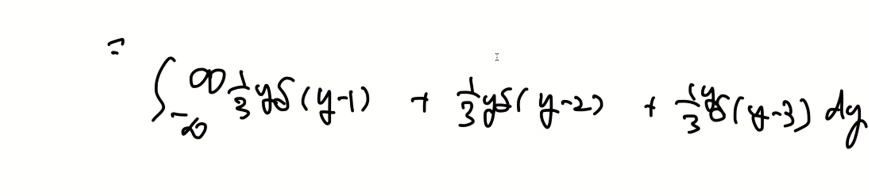
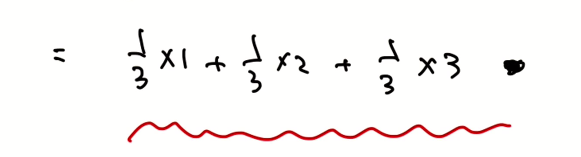
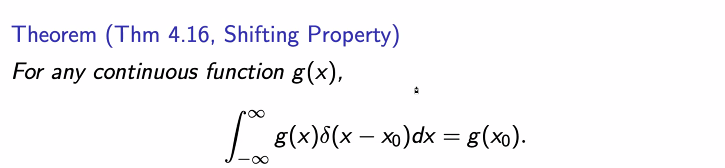
- 위와 같이 PDF로 표현이 가능하다. 하지만 이산랜덤변수는 확률을 가지고 있는 x 점에 대해 델타 함수로 표현된다.
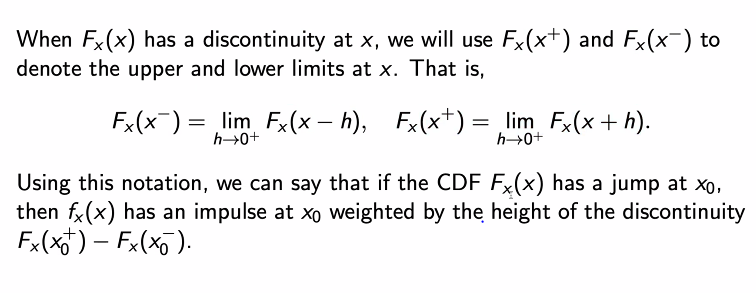
- 만약 x점에 대해 불연속이 존재한다면 x점에서의 우로부터 접근하는 것을 Fx(x+), x점에서 왼쪽에서 접근하는 것을 Fx(x-)로 정의할 수 있다.
- CDF에서 어떤 x에서 점프를 한 경우에는 Fx(x0+) - Fx(x0-)로 표현할 수 있다.
예제)
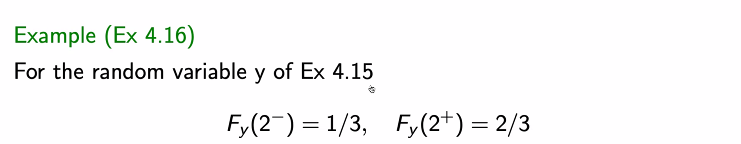
랜덤 변수 x에 대해 다음과 같이 표현할 수 있다.
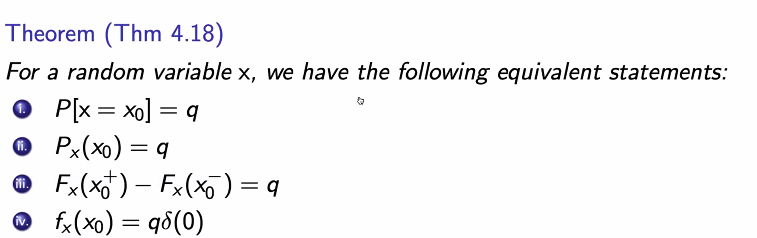
iv) X0라는 점에 대해 evaluation을 하는 것이기에 다음과 같이 표현한다.

- 치역이 countable이면 이산랜덤변수, uncountable이면 연속랜덤변수이다.
- CDF가 연속함수이면 연속랜덤변수, 그렇지 않으면 이산랜덤변수이다.
- 어떤 랜덤 변수의 PDF가 유한한 값을 가지거나 nonzero와 impulse가 있다면 이는 혼합 랜덤 변수이다.
예제)

풀이)
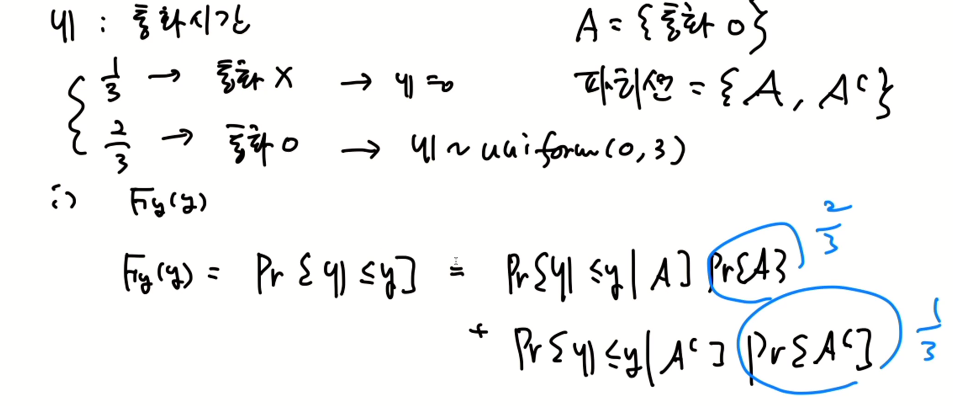
전체 확률의 법칙을 사용해 위와 같이 표현할 수 있다.
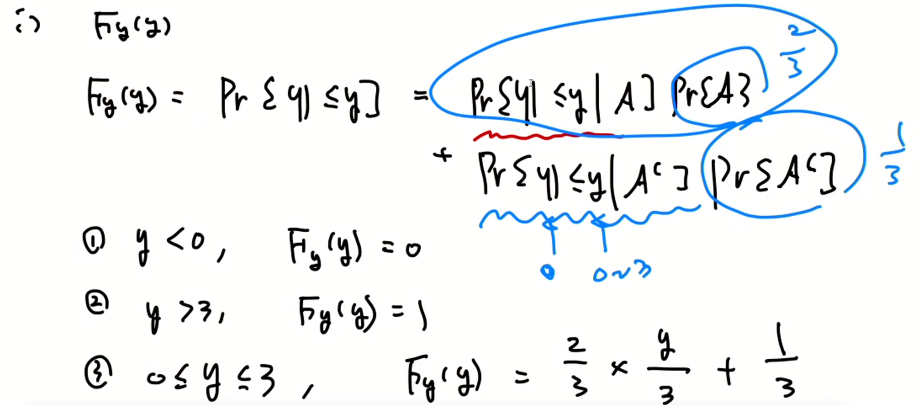
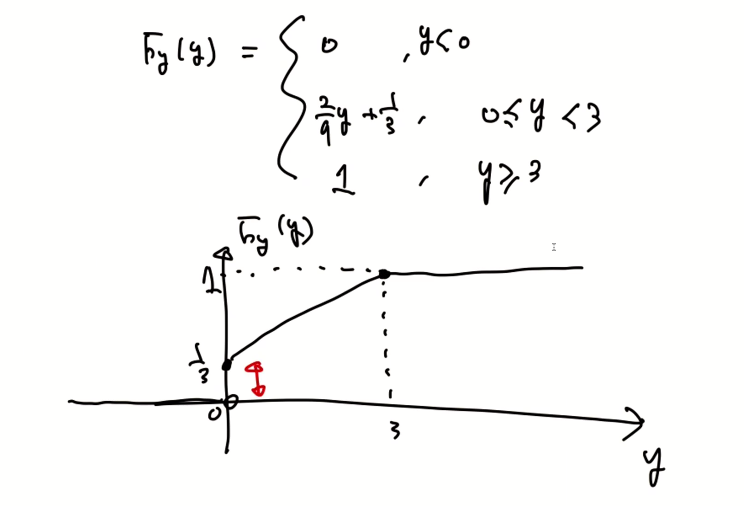
0에서 불연속 점이 존재하고, 미분을 한다면 y=0에서 impulse가 생긴다.
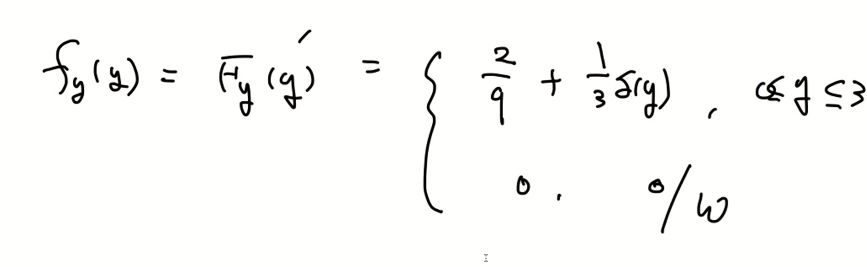
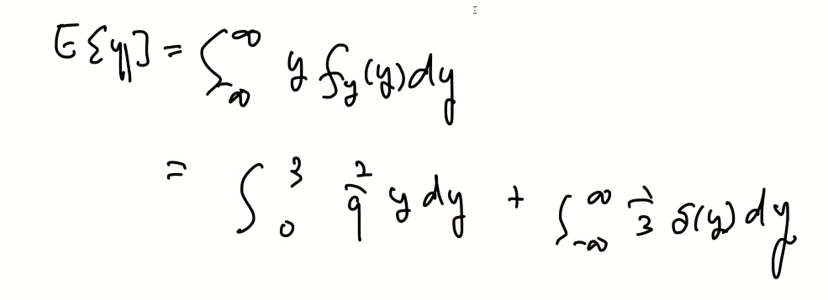
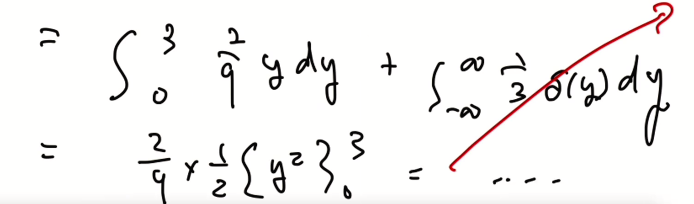
- 앞에 y가 빠졌다.
Review

- 어떤 랜덤변수든지 간에 CDF는 항상 존재한다.
- 그러나 CDF가 계단형 모양처럼 평평한 부분을 가지고, 평평한 부분 사이에 불연속 jump가 존재하는 경우에는 이산 랜덤변수이다.
- CDF가 연속이면 랜덤변수 또한 연속이다.
- CDF가 부분부분 연속이며, 중간에 불연속 점이 존재하면 그 랜덤변수는 혼합 랜덤변수이다.
- 어떤 랜덤 변수가 이산, 또는 혼합인 경우에는 그 PDF는 하나, 혹은 그 이상의 델타 함수를 포함하고 있다.

Function of RV(Derived RV)의 분포나 어떤 랜덤 변수를 가지고 있는지 궁금하다. 이를 위해 아래 두 가지 Step을 밟으면 분포를 구할 수 있다.

가장 쉬운 종류의 CDF

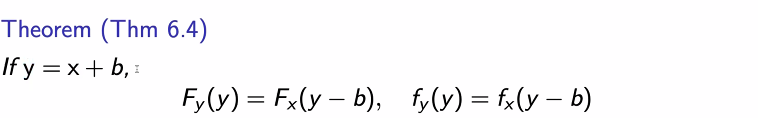
증명)
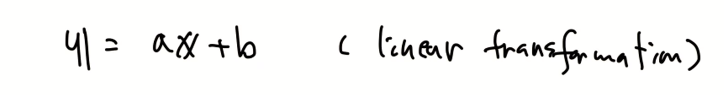
위의 내용을 linear stransformation(선형 변환)한다고 얘기한다. 이를 활용해 위의 내용을 확인할 수 있다.
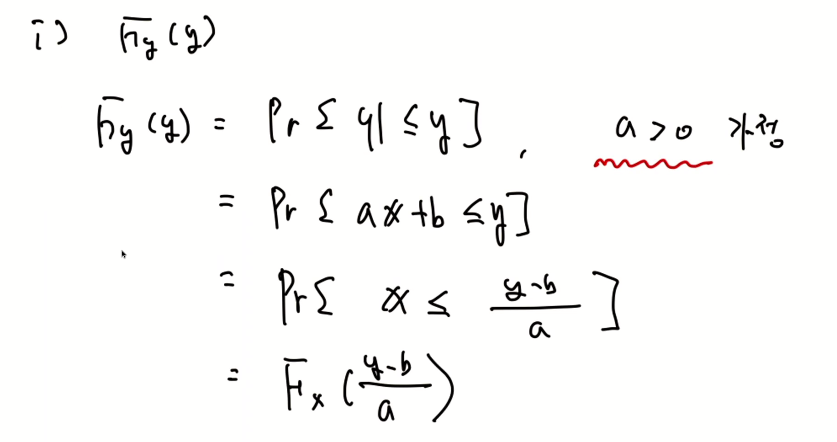
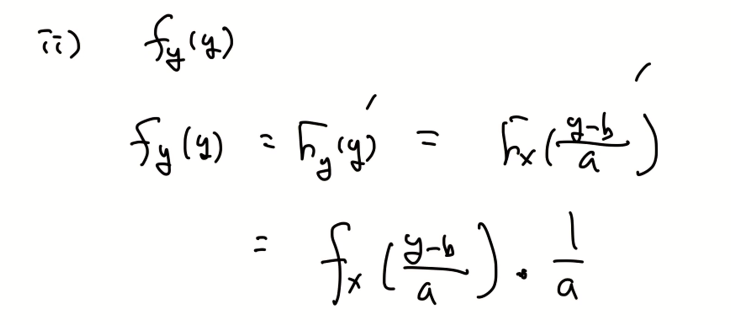
theorem 6.4는 a = 1인 경우이다.

- 파라미터 값은 변하지만 분포는 변하지 않는다.
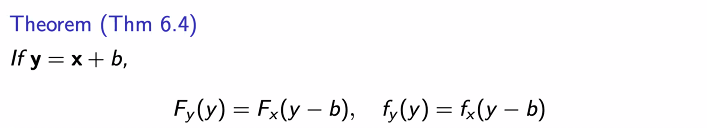
예제)
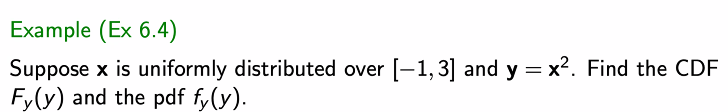
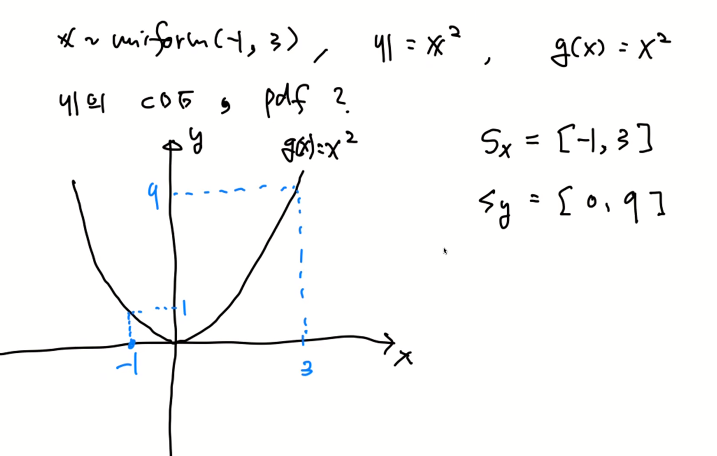
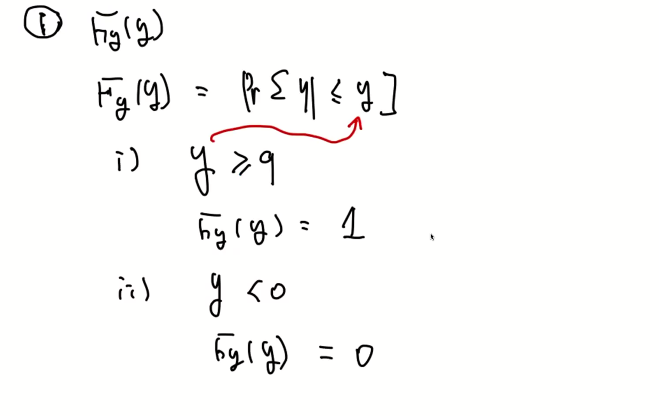
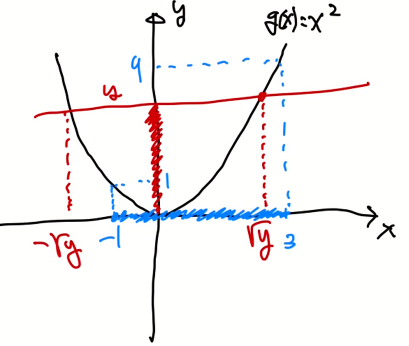
x의 치역이 -1부터 3까지이기에 다음과 같이 내용을 적을 수 있다.
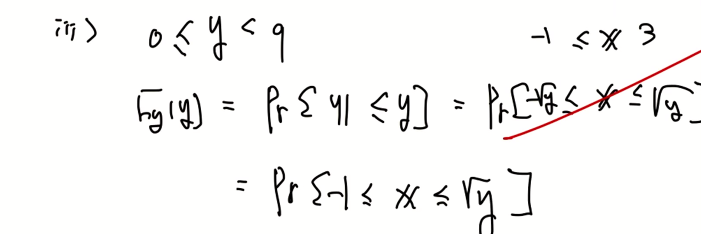
단, y가 0부터 1사이의 값을 가진다면 다음과 같은 x의 치역이 달라지게 된다. 따라서 다음과 같이 내용을 수정할 수 있다.
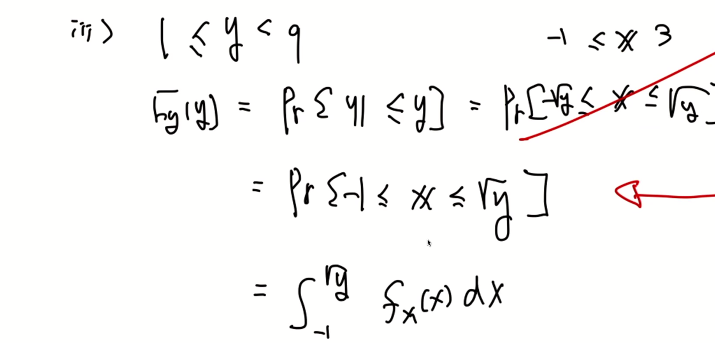
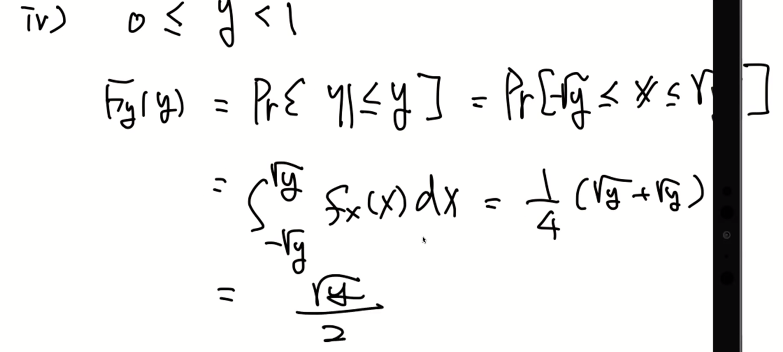
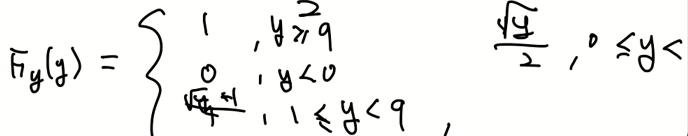

- 랜덤변수의 함수의 특정한 케이스
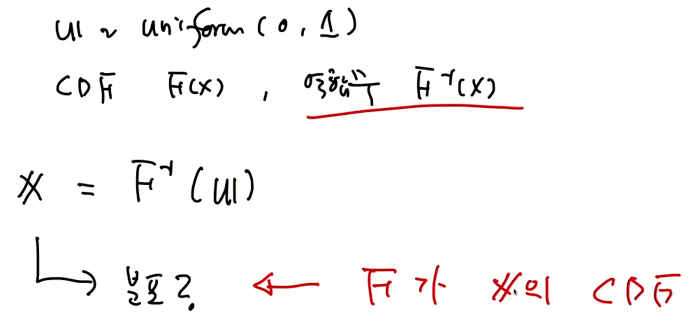
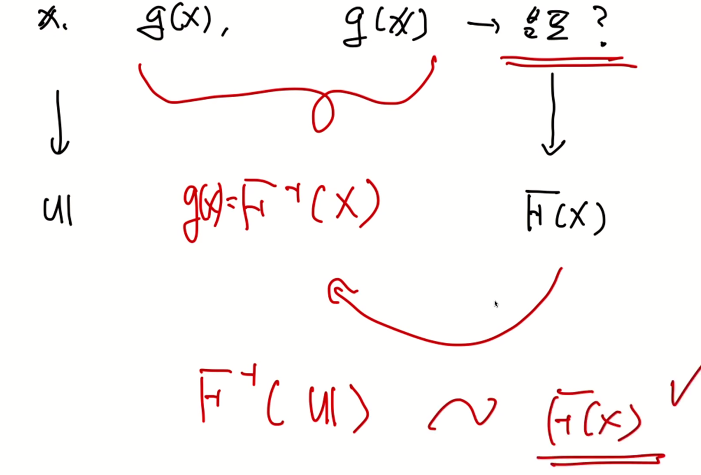
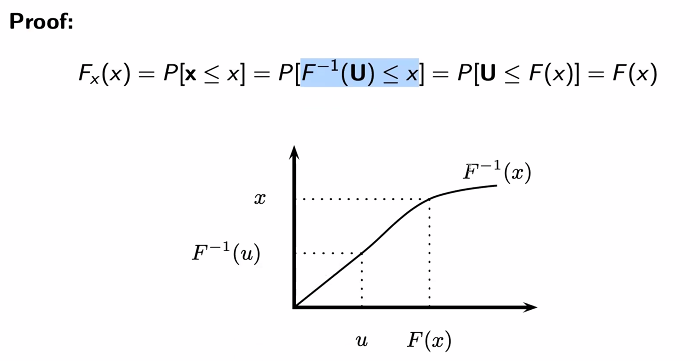
예제)

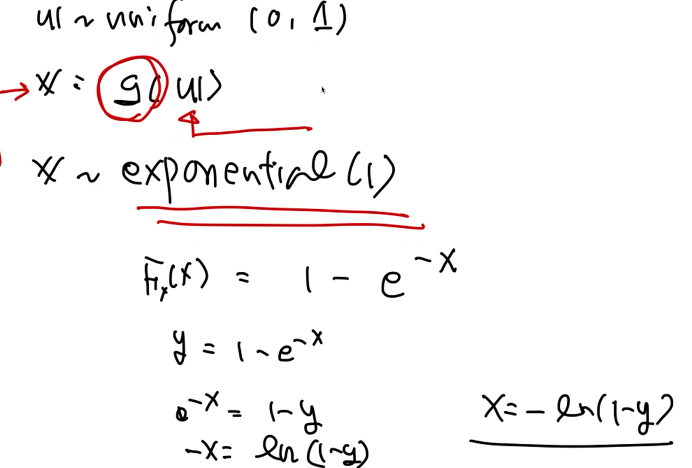
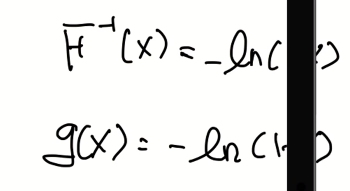
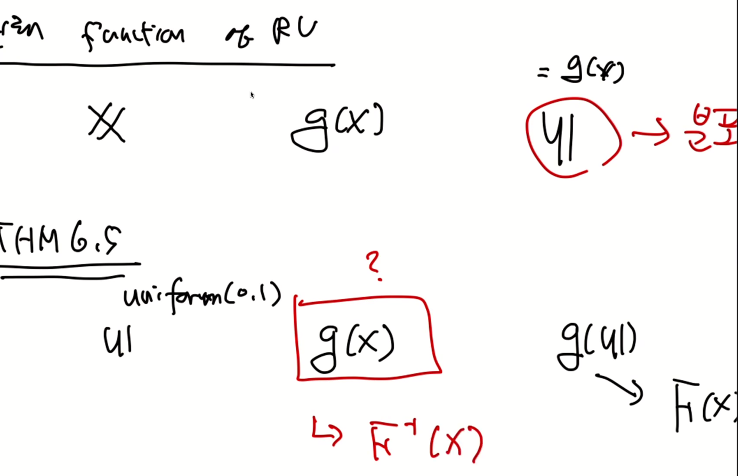
예제)

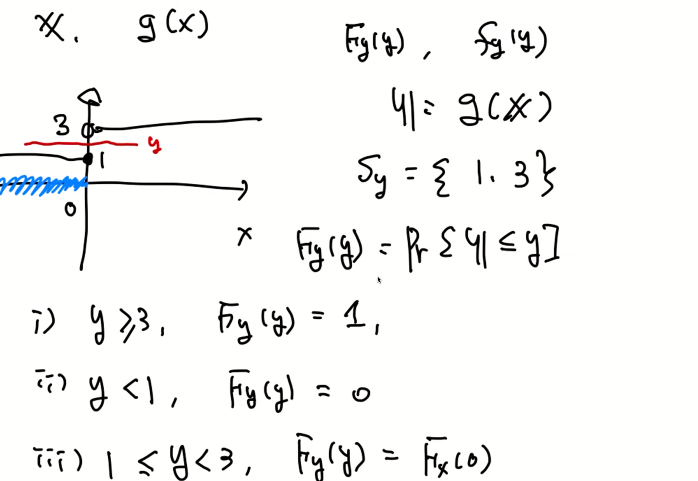
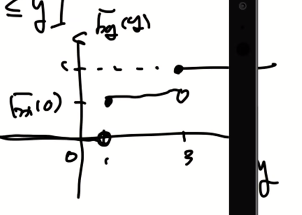
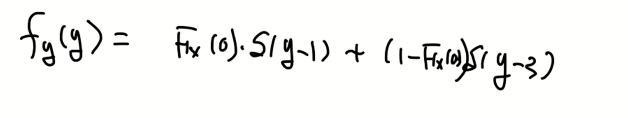
예제)

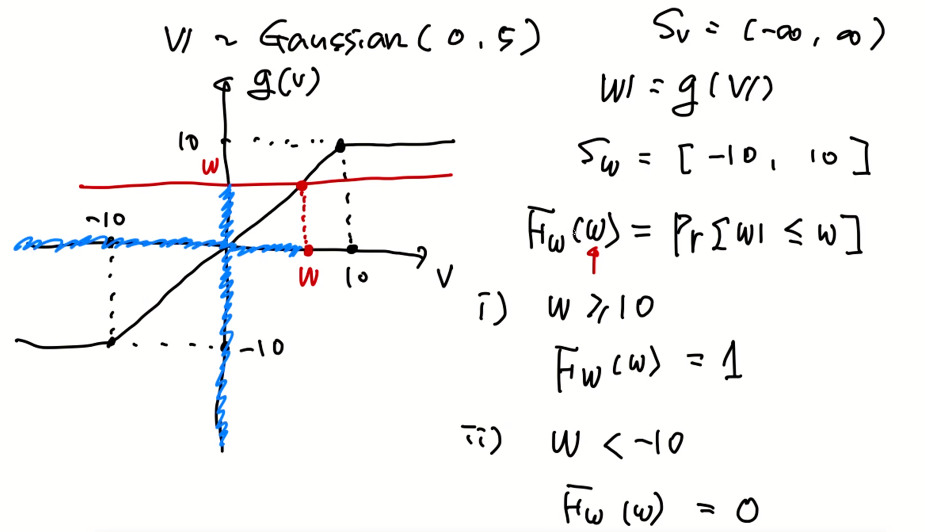
w가 나오기 위해선 v가 -10부터 w보다 작아야한다.
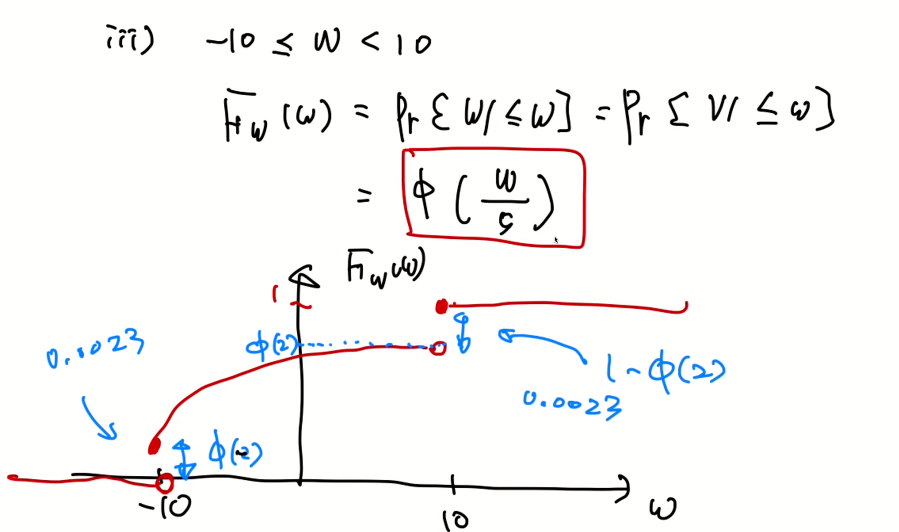
-10과 10에서 불연속 점이 존재한다.
- 파이2는 0.97725이다.
'강의 내용 정리 > 확률및랜덤변수' 카테고리의 다른 글
| 확률 및 랜덤변수(5), 통계와 확률 (0) | 2022.04.16 |
|---|---|
| 확률 및 랜덤변수 (4), 이산랜덤변수 (0) | 2022.04.15 |
| 확률 및 랜덤변수 (3), 순차 확률 (0) | 2022.03.22 |
| 확률 및 랜덤변수, 확률(2) (0) | 2022.03.07 |
| 확률 및 랜덤 변수, 확률(1) (1) | 2022.03.07 |