2022. 12. 25. 22:52ㆍ강의 내용 정리/데이터베이스
함수적 종속성 부록

Closure test
위첨자로 +를 붙여서 이를 사용한다.
Y는 어트리뷰트 집합을 의미한다.
Closure: 어트리뷰트들의 집합이 결정할 수 있는 모든 어트리뷰트를 모아놓은 것
Closure를 구하는 방법
1. 처음에는 Y+ = Y로 둔다.
ex) Y = {C, D} => Y+ = {C, D}
2. Y+에 포함된 X가 다른 어트리뷰트를 결정지으면 이를 Y+에 포함시킨다.
ex) X E Y+, X -> A => Y+에 A를 포함
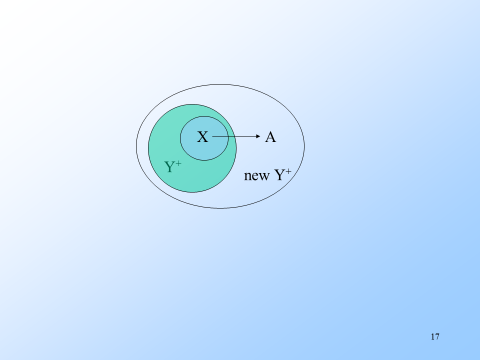
예

요구사항에 따라 ABCD를 ABC와 AD로 분해한다. 이때 ABC와 AD의 함수적종속성을 알아야한다.
ABC의 함수적 종속성: AB -> C
AD의 함수적 종속성: D -> A
분해된 릴레이션에서는 C -> D의 함수적 종속성이 사라졌다. 또한 원래 있던 함수적 종속성을 고려해보면 C -> A가 되는데 해당 함수적 종속성도 분해된 릴레이션에서는 포함할 수 없다.
위의 문제를 해결하기 위해 Closure를 구해서 이를 처리할 수 있다.
A+ = {A}
B+ = {B}
C+ = {C, D, A}
D+ = {D, A}
어트리뷰트 하나만 있는 경우의 클로저를 구한 뒤 어트리뷰트 두 개가 있는 경우의 클로저를 구한다.
AB+ = {A+, B+, C+} = {A, B, C, D}
클로저를 통해 키 값을 구할 수 있다. 가능한 모든 부분 집합에 대해 클로저를 구할 수 있다. n개의 어트리뷰트에 대해 2의 n-1개만큼 구할 수 있다. ?
cf) FD의 프로젝션
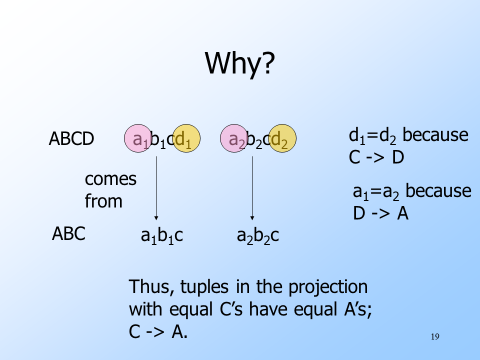
정규화 부록

Drinkers는 부분 함수적 종속성이 발생한다. 이에 따라 이를 분해한다.
Drinkers1
- BCNF -> 결정자는 키밖에 없다.
- 함수적 종속성: name -> addr / name -> favBeer
- Closure
name+ = {name, addr, favBeer}
addr+ = {addr}
favBeer+ = {favBeer}
{name, addr}+ = {name, addr, favBeer}
{name, favBeer}+ = {name, addr, favBeer}
{addr, favBeer}+ = {name, addr, favBeer}
{name, addr, favBeer}+ = {name, addr, favBeer}
Drinkers2
- 제1정규형 -> 부분 함수적 종속성이 있다.
- 함수적 종속성: beersLiked -> manf / name, beersLiked -> manf
- Closure
name+ = {name}
beersLiked+ = {beersLiked, manf}
...

Drinkers3는 BCNF가 된다.
Drinkers4는 BCNF가 된다.
분해를 할 때 지켜야하는 것

recovery: 무손실 분해가 가능해서 이를 복구 가능해야한다.
dependency preservation: 제 3정규형까지는 dependency preservation이 가능하다. 하지만 BCNF를 만들면서 이를 지키지 못할 수 있다.

AB -> C, C -> B에 대한 함수적 종속성이 사라진다. 이에 따라 도메인의 시멘틱스가 사라질 수 있기에 dependency preservation가 위배된다.
기본키에 대해서만 완전 함수적 종속성을 만족시키지 못하지만 후보키에 대해 완전 함수적 종속성을 만족시키지 못한다면 문제가 발생할 수 있다. 따라서 모든 후보키에 대해 함수적 종속성을 해결할 경우에 중복성을 제거할 수 있다.
만약 기본키에 대해서만 함수적 종속성을 해결한다면 일련번호를 통해 함수적 종속성을 해결할 수 있지만 중복성이 여전히 남아있을 수 있다. 따라서 기본키에 대해서만 함수적 종속성을 해결할 경우에는 중복성을 제거할 수 없다.
'강의 내용 정리 > 데이터베이스' 카테고리의 다른 글
| 데이터베이스(13), 트랜잭션 (0) | 2023.02.05 |
|---|---|
| 데이터베이스(12), 뷰와 시스템 카탈로그 (0) | 2023.01.31 |
| 데이터베이스(10), 릴레이션 정규화 (0) | 2022.12.20 |
| 데이터베이스(9), 물리적 데이터베이스 설계 (1) | 2022.12.14 |
| 데이터베이스(8), 데이터베이스 설계와 ER 모델 (1) | 2022.12.13 |