2020. 12. 31. 18:00ㆍEnglish/Machine learning algorithm
1. Mathematical definitions of artificial neurons
Prior to implementing Perceptron, the mathematical definition of Perceptron must precede.
The Perceptron we want to implement is simply a binary classification task with two classes. Defines the determination function by linear combination of the input value x and corresponding weight vector w. Linear combinations have organized concepts in different postings(in Korean).
Anyway, the final z is determined by the multiplication between the transpose vector of the weight vector W and the vector of X. If the z that is last entered is greater than a certain threshold, assign it as 1, if it is less than -1. We'll update the weight by comparing it to the actual value. You will continue to modify the weights as you repeat this process, while predicting classes.
To sum up this process briefly,
1. Initialize weights to zero or randomly small values.
2. Proceed to the next task of each training sample drawer.
a. Calculates the output value yhat.
b. Update weights.
can be expressed as
Now let's start implementing the perceptron.
2. Implementing a perceptron
Load the required library and data.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inlinetrain = pd.read_csv('./titanic/train.csv')
test = pd.read_csv('./titanic/test.csv')
train.head()
Previously, during the Titanic project at Kaggle, Titanic data set was saved in a personal folder. This was imported and saved.
Feature engineering is a very important step, but I also referred to the previous feature engineering! If you are curious, please refer to my Titanic posting.
# concate dataset(train, test)
df = pd.concat(objs = [train, test], axis = 0).reset_index(drop = True)
# fill null-values in Age
age_by_pclass_sex = df.groupby(['Sex', 'Pclass'])['Age'].median()
df['Age'] = df.groupby(['Sex', 'Pclass'])['Age'].apply(lambda x: x.fillna(x.median()))
# create Cabin_Initial feature
df['Cabin_Initial'] = df['Cabin'].apply(lambda s: s[0] if pd.notnull(s) else 'M')
df['Cabin_Initial'] = df['Cabin_Initial'].replace(['A', 'B', 'C', 'T'], 'ABCT')
df['Cabin_Initial'] = df['Cabin_Initial'].replace(['D', 'E'], 'DE')
df['Cabin_Initial'] = df['Cabin_Initial'].replace(['F', 'G'], 'FG')
df['Cabin_Initial'].value_counts()
# fill null-values in Embarked
df['Embarked'] = df['Embarked'].fillna('S')
# fill null-values in Fare
df['Fare'] = df['Fare'].fillna(df.groupby(['Pclass', 'Embarked'])['Fare'].median()[3]['S'])
# binding function for Age and Fare
def binding_band(column, binnum):
df[column + '_band'] = pd.qcut(df[column].map(int), binnum)
for i in range(len(df[column + '_band'].value_counts().index)):
print('{}_band {} :'.format(column, i), df[column + '_band'].value_counts().index.sort_values(ascending = True)[i])
df[column + '_band'] = df[column + '_band'].replace(df[column + '_band'].value_counts().index.sort_values(ascending = True)[i], int(i))
df[column + '_band'] = df[column + '_band'].astype(int)
return df.head()
binding_band('Age',8)
binding_band('Fare', 6)
# create Initial feature
df['Initial'] = 0
for i in range(len(df['Name'])):
df['Initial'].iloc[i] = df['Name'][i].split(',')[1].split('.')[0].strip()
Mrs_Miss_Master = []
Others = []
for i in range(len(df.groupby('Initial')['Survived'].mean().index)):
if df.groupby('Initial')['Survived'].mean()[i] > 0.5:
Mrs_Miss_Master.append(df.groupby('Initial')['Survived'].mean().index[i])
elif df.groupby('Initial')['Survived'].mean().index[i] != 'Mr':
Others.append(df.groupby('Initial')['Survived'].mean().index[i])
df['Initial'] = df['Initial'].replace(Mrs_Miss_Master, 'Mrs/Miss/Master')
df['Initial'] = df['Initial'].replace(Others, 'Others')
# create Alone feature
df['Alone'] = 0
df['Alone'].loc[(df['SibSp'] + df['Parch']) == 0] = 1
# create Companinon's survival rate feature
df['Ticket_Number'] = df['Ticket'].replace(df['Ticket'].value_counts().index, df['Ticket'].value_counts())
df['Family_Size'] = df['Parch'] + df['SibSp'] + 1
df['Companion_Survival_Rate'] = 0
for i, j in df.groupby(['Family_Size', 'Ticket_Number'])['Survived'].mean().index:
df['Companion_Survival_Rate'].loc[(df['Family_Size'] == i) & (df['Ticket_Number'] == j)] = df.groupby(['Family_Size', 'Ticket_Number'])["Survived"].mean()[i, j]
comb_sum = df.loc[df['Family_Size'] == 5]['Survived'].sum() + df.loc[df['Ticket_Number'] == 3]['Survived'].sum()
comb_counts = df.loc[df['Family_Size'] == 5]['Survived'].count() + df.loc[df['Ticket_Number'] == 3]['Survived'].count()
mean = comb_sum / comb_counts
df['Companion_Survival_Rate'] = df['Companion_Survival_Rate'].fillna(mean)
# select categorical features
cate_col = []
for i in [4, 11, 12, 15]:
cate_col.append(df.columns[i])
cate_df = pd.get_dummies(df.loc[:,(cate_col)], drop_first = True)
df = pd.concat(objs = [df, cate_df], axis = 1).reset_index(drop = True)
df = df.drop(['Name', 'Sex', 'Age', 'Ticket', 'Fare', 'Embarked', 'Cabin_Initial', 'SibSp', 'Parch',
'Cabin', 'Initial', 'Ticket_Number', 'Family_Size'], axis = 1)
# split data
df = df.astype(float)
train = df[:891]
test = df[891:]
train_X = train.drop(['Survived', 'PassengerId'], axis = 1)
train_y = train.iloc[:, 1]
test_X = test.drop(['Survived', 'PassengerId'], axis = 1)
And now let's start implementing Perceptron.
class Perceptron(object):
def __init__(self, eta = 0.01, n_iter = 50, random_state = 1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc = 0, scale = 0.01,
size = 1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for i in range(len(X)):
xi = X.iloc[i].values
target = y[i]
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def predict(self, X):
return np.where(self.net_input(X) >= 0.0, 1, 0)
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]I was able to write algorithms more simply than I thought. I'll briefly describe the parameters and properties used in that class.
- eta : Learning rate (float)
- n_iter : Number of repetitions of training data (int)
- random_state : Random number (int)
- w_ : Learned weight (1d-array)
- errors_ : Classification errors accumulated per epoch (list)
- X : Training data
- y : Target value
Proceed in the manner described above. Let's look at the sequence of the code.
1. Set the initial w_ (weight value). The number of input variable is as large as + 1, which randomly consists of a normal distribution value based on zero.
2. Jump Xi and w_[1:] to np.dot and store the value added to w_[1] as the final input value. The concept of jumbo can be found in the posting of basic components of linear regression. The method of multiplication calculation between matrices is briefly described in the corresponding posting.
3. If the final input value is greater than 0, print out 0 if it is less than or equal to or less than 0. Unlike the above explanation, the target variable is made up of values of 0 and 1.
4. If the final output of the predicted value (yhat) is the same as the actual value, the update will be zero and the first prediction will be finished without modifying the weights. If the predicted and actual values differ, the update stores the eta (learning rate), which is added to w_[1], and the values multiplied by eta and xi are added to w_[1:]. Then save it in error.
Repeat 5.2-4 and add errors to errors_.
6. Repeat 1-5 for the given n_iter.
7. Print the self.
It is an algorithm that can be implemented less complex than expected. We learned this in the train set and figured out the accuracy according to the number of iterations.
# 학습
Pc = Perceptron(n_iter = 100)
Pc.fit(train_X, train_y)
# 그래프
fig = plt.subplots(figsize = (15, 8))
plt.plot(range(1, len(Pc.errors_) + 1), Pc.errors_)
plt.legend(['Perceptron errors'], loc = 'upper right')
plt.xlabel('Epoch', fontsize = 10)
plt.ylabel('Number of errors', fontsize = 10)
plt.show()
After 7 to 8 studies, the number of errors dropped to about 200, and then the number of errors converging to 190 to 210 afterwards.
3. Implementing a coordinated perceptron
So far, this is what came out of this textbook. Suddenly, I was wondering if there was a way to supplement this method, and I wondered if I could set the initial w_value differently. So we decided to add the initial w_value to the correlation value between each variable and target variable. First of all, the correlation is directly related to target variability, so I thought that if you adjust this value, you can predict it faster and more accurately than the Perceptron written in the book. Also, the correlation with 'Survived' (target variable) has values from 0 to 1 so I thought it would be possible to reflect the relationship with target variable well without scale problems. Here's the Adjusted Perceptron algorithm that we created.
class Adjusted_Perceptron(object):
def __init__(self, eta = 0.01, n_iter = 50, random_state = 1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
cor_X = X.copy()
cor_y = y.copy()
cor_X['Target'] = cor_y
self.w_ = [cor_X.corr()['Target'].values[i]
for i in range(len(cor_X.corr()['Target'].values))
if cor_X.corr()['Target'].index[i] != 'Target']
self.w_.insert(0, 0)
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for i in range(len(X)):
xi = X.iloc[i].values
target = y[i]
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def predict(self, X):
return np.where(self.net_input(X) >= 0.0, 1, 0)
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
I predicted the train set with the Adjusted Perceptron and drew a graph to see the difference between Perceptron and Perceptron and Perceptron.
# 학습
APc = Adjusted_Perceptron(n_iter = 100)
APc.fit(train_X, train_y)
# 그래프
fig = plt.subplots(figsize = (15, 8))
plt.plot(range(1, len(APc.errors_) + 1), APc.errors_)
plt.plot(range(1, len(Pc.errors_) + 1), Pc.errors_)
plt.legend(['Adjusted_Perceptron', 'Perceptron'], loc = 'upper right')
plt.title('Adjusted Perceptron vs Perceptron', fontsize = 20)
plt.xlabel('Epoch', fontsize = 10)
plt.ylabel('Number of errors', fontsize = 10)
plt.show()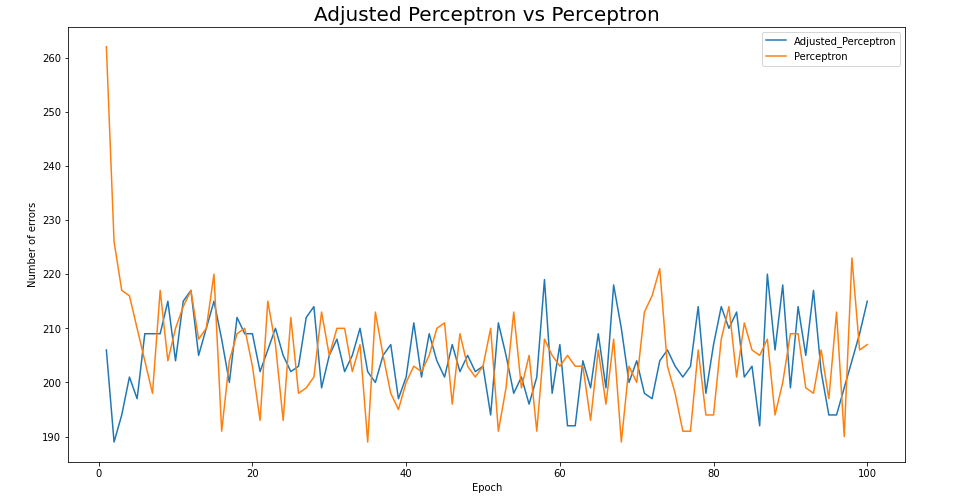
The results were more interesting than I thought. Adjusted Perceptron did not differ much from what was learned more than once or twice. This is the result of setting the initial setting as correlation and proceeding with the prediction. This is the biggest difference from Perceptron. And if there's a lot of learning data, it means that in terms of learning time, the Adjusted Perceptron can be a much better algorithm. When I saw that my own algorithms were better than time costs, I was able to achieve a greater sense of accomplishment than I thought.
We also selected the appropriate number of iterations for each algorithm and submitted the predicted value to the kaggle to check the public acuity.
Pc = Perceptron(n_iter = 10)
Pc.fit(train_X, train_y)
predict = [Pc.predict(test_X)]
APc = Adjusted_Perceptron(n_iter = 2)
APc.fit(train_X, train_y)
predict.append(APc.predict(test_X))
for i in range(len(predict)):
submission = pd.DataFrame(columns = ['PassengerId', 'Survived'])
submission['PassengerId'] = df['PassengerId'][891:].map(int)
submission['Survived'] = predict[i]
submission.to_csv('my_submission_{}.csv'.format(i + 1), header = True, index = False)Accuracy:
Perceptron : 0.75358
Adjusted Perceptron : 0.75837
Ensemble : 0.76794
Ensemble is the result of previously submitted combinations of classification algorithms. However, the accuracy of Perceptron and Adjusted Perceptron is not that bad. Of course, if you have to classify complex data, you may have a big difference in accuracy, but I think it's a pretty good model for Titanic.
We've implemented Perceptron from the book and Perceptron, which we've adjusted the parameters directly. In the next posting, we will implement Adalin, an adaptive linear New Ryon classifier.
'English > Machine learning algorithm' 카테고리의 다른 글
| [6] Information gain and impurity of decision tree (0) | 2021.01.06 |
|---|---|
| [5] Non-linear Troubleshooting with Kernel SVM (0) | 2021.01.04 |
| [4] Understand Support Vector Machine (SVM) Principles (linear) (0) | 2020.12.31 |
| [3] Logistic Regression Principles (0) | 2020.12.31 |
| [2] Implement Adaline (adaptive linear neuron) (0) | 2020.12.31 |